3400Km

考点：

专题：万有引力定律的应用专题．

分析：此题为卫星做圆周运动的基本计算型题目，借助万有引力定律和运动学公式找出卫星距离地面的高度和常量之间的关系；为了避开地球质量问题，可以借助一地球表面某物体的重力可看做是和地球之间的万有引力去解决．

解答：解：设地球质量M，地球半径R，卫星距离地面高度h，卫星质量m，当航天飞机接近这颗卫星并与他运行情况基本相同时，速度达到了v=6.4km/s，说明卫星的运行速度也是v=6.4km/s，卫星在天上时，由万有引力提供向心力，所以：G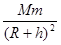=m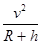  

转换公式可得：v²=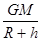                        ①，另设地球表面上有一物体，质量为m₁，那么它在地球表面受到的万有引力就是其重力所以，m₁g=G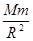， 转换公式可得：GM=R²g                        ②

将②代入①得到：v²=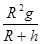       即 h=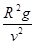-R，将已知数据代入，得到：h="3400km"

故这颗卫星离地面的高度为3400km

点评：此题为卫星做圆周运动的基本计算型题目，主要考查万有引力充当向心力的相关应用和计算，为中档题．