问题
解答题
设f（x）是定义在R上的奇函数，g（x）与f（x）的图象关于直线x=1对称，若g（x）=a（x﹣2）﹣（x﹣2）3．
（1）求f（x）的解析式；
（2）当x=1时，f（x）取得极值，证明：对任意x1，x2∈（﹣1，1），不等式|f（x1）﹣f（
x2）|＜4恒成立；
（3）若f（x）是[1，+∞）上的单调函数，且当x0≥1，f（x0）≤1时，有f[f（x0）]=x0，求证：
f（x0）=x0．
答案
解：（1）∵f（x）与g（x）的图象关于x=1对称，
设点M（x，f（x））是f（x）上的任意一点．
则点M关于x=1的对称点（2﹣x，g（2﹣x））在函数g（x）的图象上．
∴f（x）=g（2﹣x）=﹣ax+x3．
（2）f′（x）=﹣a+3x2，又x=1是函数f（x）的一个极值点，
∴f′（1）=0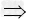
﹣a+3=0，得a=3，
故f（x）=﹣3x+x3．f′（x）=﹣3+3x2=﹣3（x+1）（x﹣1），
当x∈[﹣1，1]，f′（x）≤0， ∴f（x）在[﹣1，1]上是减函数．
fmin（x）=f（1）=﹣2，fmax（x）=f（﹣1）=2，
故对任意x1，x2∈（﹣1，1），有|f（x1）﹣f（x2）|＜|2﹣（﹣2）|=4．
（3）若f（x）在[1，+∞）是减函数，则f′（x）=﹣a+3x2＜0在[1，+∞）上恒成立．
即a≥3x2在[1，+∞）上恒成立，此时a不存在；
若f（x）在[1，+∞）是增函数，即a≤3x2在[1，+∞）上恒成立．故a≤3．
设f（x0）＞x0≥1则f[f（x0）]＞f（x0），
∴x0＞f（x0）矛盾，
若x0＞f（x0）≥1则f（x0）＞f[f（x0）]
∴f（x0）＞x0矛盾！故f（x0）=x0．