问题
计算题
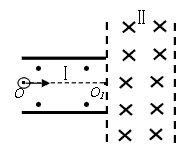
如图所示在两极板间存在匀强电场和磁感应强度为B的匀强磁场Ⅰ，一带电量为+q，质量为m的粒子恰能以速度υ沿OO1 匀速飞出极板，进入磁感应强度为2B的匀强磁场区域Ⅱ。不计粒子重力，求：
(1)两极板间匀强电场的电场强度的大小和方向；
(2)粒子经过磁场Ⅱ后从左边界射出的位置S距O1的距离；
(3)若撤去两极板间的电场，粒子仍以水平速度υ从O点释放， 偏转后恰能从下极板右端飞出，并经过磁场Ⅱ后回到O点。已知极板间距为2d，求磁场Ⅱ的宽度至少为多少？
答案
解：
1）由题可知粒子在极板间受电场力和洛伦兹力平衡，由粒子带正电可得电场强度方向竖直向上，设大小为E，有：
①
解得：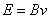
2）从O1进入磁场Ⅱ偏转后从点S飞出，如图，设轨道半径为R2，由几何关系得：
②
又
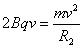③
解得：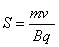
3)由题可知撤去电场后粒子恰能飞出极板并回到O点， 其轨迹如图所示：
设在磁场Ⅰ中偏转半径为R1，则：
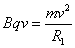④
联立③④得：
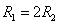⑤
由几何关系得：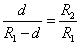
⑥
联立⑤⑥解得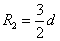
⑦
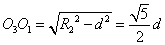⑧
故磁场Ⅱ区域的宽度至少为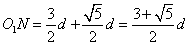
⑨。