问题
问答题
右图是一个设计“过山车”的试验装置的工作原理示意图，光滑斜面与竖直平面内的圆形轨道的最低点B平滑连接，圆形轨道半径为R，一质量为m的小车(可视为质点)在A点由静止释放并沿斜面滑下，当小车第一次经过B点进入圆形轨道时对轨道B点的压力为其所受重力的7倍，小车恰能越过圆形轨道最高点C完成圆周运动并第二次经过最低点B再沿水平轨道向右运动。已知重力加速度的大小为g。
(1)求A点距水平面的高度h；
(2)假设小车在竖直圆轨道的左、右半圆轨道部分克服摩擦阻力做功相等，求小车第二次经过 圆轨道最低点B时速度有多大?
答案
（1）
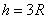（2）
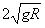
（1）依题意，在B点应用牛顿第二定律有
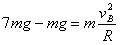…………………①（３分）
由机械能守恒定律有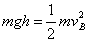
………………②（３分）
由①、②两式解得A点距水平面的高度为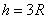： …………③（２分）
（2）依题意，在C点应用牛顿第二定律有：
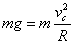………………………④（３分）
则小车从B到C的过程中，克服摩擦阻力做功为
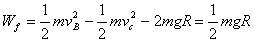……………⑤（３分）
从C到B的过程中应用动能定理有
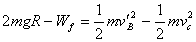………………………⑥（３分）
解得小车第二次经过圆轨道最低点B时的速度为：
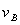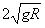′＝ …………………⑦（２分）