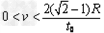问题
计算题
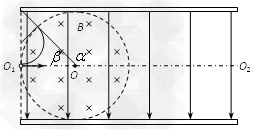
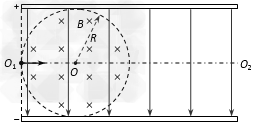
如图所示，带电平行金属板相距为2R，在两板间有垂直纸面向里、磁感应强度为B的圆形匀强磁场区域，与两板及左侧边缘线相切。一个带正电的粒子（不计重力）沿两板间中心线O1O2从左侧边缘O1点以某一速度射入，恰沿直线通过圆形磁场区域，并从极板边缘飞出，在极板间运动时间为t0。若撤去磁场，质子仍从O1点以相同速度射入，则经t0/2时间打到极板上。
（1）求两极板间电压U；
（2）若两极板不带电，保持磁场不变，该粒子仍沿中心线O1O2从O1点射入，欲使粒子从两板左侧间飞出，射入的速度应满足什么条件。
答案
解：（1）设粒子从左侧O1点射入的速度为v0，极板长为L
粒子在初速度方向上做匀速直线运动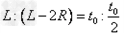
，
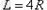
在电场中：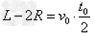
在复合场中作匀速运动：
解得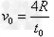
，
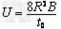
（2）设粒子在磁场中做圆周运动的轨道半径为r，粒子恰好从上极板左边缘飞出时速度的偏转角为α，由几何关系可知：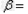
，
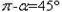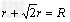
因为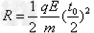
，所以
根据向心力公式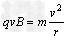
，解得 r=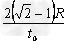
所以，粒子两板左侧间飞出的条件为
