问题
计算题
| 如图所示，xOy平面内半径为R的圆O'与y轴相切于坐标原点O，在该圆形区域内，有与y轴平行向下的匀强电场和垂直于圆面向外的匀强磁场，若只加匀强电场或只加匀强磁场，一个带负电的小球从原点O以一定的初速度沿x轴进入圆形区域，小球恰好做匀速直线运动，若电场和磁场都撤去，其他条件不变，该带电小球穿过圆形区域的时间恰好为做匀速直线运动穿过圆形区域时间的一半，重力加速度为g，求： |
| (1)小球的初速度； |
| (2)电场强度与磁感应强度的比值； |
| (3)若电场和磁场都存在，其他条件不变，那么，该带电小球穿过圆形区域的时间。 |
 |
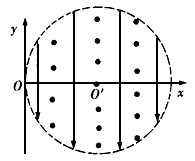答案
解：
(1)若电场和磁场都撤去，由题意知小球做平抛运动，故有：
水平位移R=v0t
竖直位移R=gt2/2
联立解出v0=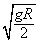
‘
(2)设电场强度为E，磁感应强度为B，只加匀强电场或只加匀强磁场，小球恰好做匀速直线运动，故
qE=mg
qv0B=mg
再联立v0=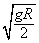
，解得E/B=
；
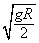(3)若电场和磁场都存在，其他条件不变，因为qE=mg，带电小球受合力为洛伦兹力，故带电小球做匀速圆周运动，设半径为r，从图中N点离开磁场，P为轨迹圆弧的圆心。
qv0B=mv02／r
又qv0B=mg
联立解得r=R/2
由图tanθ=R/r
带电小球在磁场中运动的时间t= 2θ/ω
又ω=v0/r
联立解得t=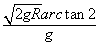
。