问题
选择题
在平行四边形ABCD中,AC与DB交于点O,E是线段OD的中点,AE延长线与CD交于F.若
|
答案
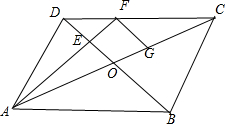
∵由题意可得△DEF∽△BEA,
∴
=DE EB
=DF AB
,再由AB=CD可得 1 3
=DF DC
,1 3
∴
=DF FC
.1 2
作FG平行BD交AC于点G,
∴
=FG DO
=CG CO
,2 3
∴
=GF 2 3
=OD 1 3
=BD 1 3
. b
∵
=AG
+AO
=OG
+AO 1 3
=OC 1 2
+AC 1 6
=AC 2 3
=AC 2 3
,a
∴
=AF
+AG
=GF 2 3
+a 1 3
,b
故选B.
