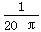问题
计算题
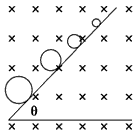
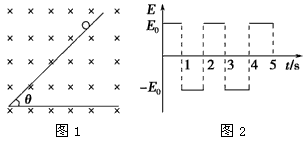
在如图1所示的空间里,存在垂直纸面向里的匀强磁场,磁感应强度为B=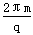 。在竖直方向存在交替变化的匀强电场,如图2所示(竖直向上为正),电场大小为E0=
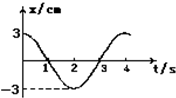
。在竖直方向存在交替变化的匀强电场,如图2所示(竖直向上为正),电场大小为E0=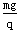 。一倾角为θ长度足够长的光滑绝缘斜面放置在此空间。斜面上有一质量为m,带电荷量为-q的小球,从t=0时刻由静止开始沿斜面下滑,设第5 s内小球不会离开斜面,重力加速度为g。求:
。一倾角为θ长度足够长的光滑绝缘斜面放置在此空间。斜面上有一质量为m,带电荷量为-q的小球,从t=0时刻由静止开始沿斜面下滑,设第5 s内小球不会离开斜面,重力加速度为g。求:
(1)第6 s内小球离开斜面的最大距离;
(2)第19 s内小球未离开斜面,θ角的正切值应满足什么条件?
答案
解:(1)设第一秒内小球在斜面上运动的加速度为a,由牛顿第二定律得:(mg+qE0)sinθ=ma ①
第一秒末的速度为:v=at1 ②
在第二秒内:qE0=mg ③
所以小球将离开斜面在上方做匀速圆周运动,则由向心力公式得qvB=m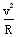 ④
④
圆周运动的周期为:T=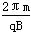 =1 s ⑤
=1 s ⑤
由题图可知,小球在奇数秒内沿斜面做匀加速运动,在偶数秒内离开斜面做完整的圆周运动。所以,第五秒末的速度为:v5=a(t1+t3+t5)=6gsin θ ⑥
小球离开斜面的最大距离为:d=2R3 ⑦
由以上各式得:d=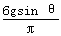
(2)第19秒末的速度:v19=a(t1+t3+t5+t7+…+t19)=20gsin θ ⑧
小球未离开斜面的条件是:qv19B≤(mg+qE0)cos θ ⑨
所以:tanθ≤