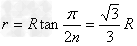问题
计算题
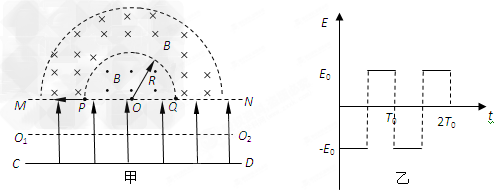
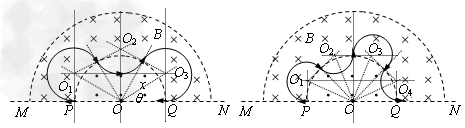
如图甲所示，CD和MN之间存在着变化的电场，电场变化规律如图乙所示（图中电场方向为正方向），MN为一带电粒子可以自由通过的理想边界，直线MN下方无磁场，上方两个同心半圆内存在着有理想边界的匀强磁场，其分界线是半径为R和2R的半圆，半径为R的圆两侧的磁场方向相反且垂直于纸面，磁感应强度大小都为B。现有一质量为m、电荷量为q的带负电微粒在t=0时刻从O2点沿MN、CD间的中心线O2O1水平向左射入电场，到达P点时以水平向左的速度进入磁场，最终打在Q点。不计微粒的重力。求：
（1）微粒在磁场中运动的周期T；
（2）微粒在电场中的运动时间t1与电场的变化周期T0之间的关系；
（3）MN、CD之间的距离d；
（4）微粒在磁场中运动的半径r的可能值的表达式及r的最大值。
答案
解：（1）洛仑兹力提供向心力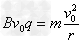
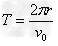
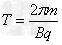
（2）由题意分析可知：微粒在竖直方向的运动加速和减速的时间是相等的
则t1=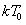
（k=1，2，3…）
（3）微粒运动的加速度大小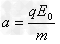
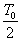时间内带电粒子的位移大小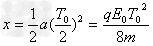
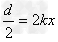（k=1，2，3…）
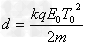（k=1，2，3…）
（4）粒子的运动轨迹将磁场边界分成n等分（n=2，3，4…）
由几何知识可得：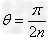
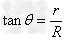
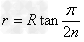
由于有边界限制，须有：x+r<2R
由几何关系可知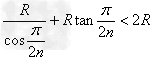
则有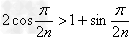
得到当n=2时不成立，如图，故n=3，4，5…
经分析可知，n越大，r就越小
当n=3时，半径r有最大值，最大值