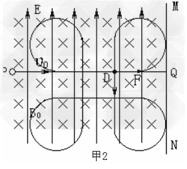
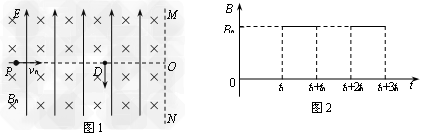
如图1所示,与纸面垂直的竖直面MN的左侧空间中存在竖直向上场强大小为E=2.5×102N/C的匀强电场(上、下及左侧无界)。一个质量为m=0.5kg、电量为q=2.0×10-2 C的可视为质点的带正电小球,在t=0时刻以大小为v0的水平初速度向右通过电场中的一点P,当t=t1时刻在电场所在空间中加上一如图2所示随时间周期性变化的磁场,使得小球能竖直向下通过D点,D为电场中小球初速度方向上的一点,PD间距为L,D到竖直面MN的距离DQ为L/π。设磁感应强度垂直纸面向里为正。(g=10m/s2)
(1)如果磁感应强度B0为已知量,使得小球能竖直向下通过D点,求磁场每一次作用时间t0的最小值(用题中所给物理量的符号表示);
(2)如果磁感应强度B0为已知量,试推出满足条件的时刻t1的表达式(用题中所给物理量的符号表示);
(3)若小球能始终在电磁场所在空间做周期性运动,则当小球运动的周期最大时,求出磁感应强度B0及运动的最大周期T的大小(用题中所给物理量的符号表示)。
解:(1)当小球进入电场时:mg=Eq将做匀速直线运动;在t1时刻加入磁场,小球在时间t0内将做匀速圆周运动,圆周运动周期为T0;若竖直向下通过D点,由图甲1分析可知必有以下:t0=3T0/4 =6πm/4qB0
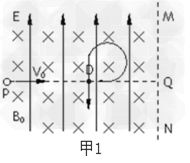
(2)PF-PD=R,即:V0t1-L=R
qV0B0=mV02/qB0
所以:V0t1-L=mV0/qB0
t1=L/V0+m/qB0
(3)小球运动的速率始终不变,当R变大时,T0也增加,小球在电场中的运动的周期T增加,在小球不飞出电场的情况下,当T最大时有:
DQ=2R,L/π=2mV0/qB0,B0=2πmV0/qL,T0=2πR/V0=2πm/qB0=L/V0
由图分析可知小球在电场中运动的最大周期:T=8×3T0/4=6L/V0
小球运动轨迹如图甲2所示