①第一眼看到那片浩大的墓地的时候,我以为看到了正在安闲地吃着青草的一群羊。那些伫立在草地上的白色十字架,连绵在一起,远远一望,像极了雪白的羊群。我悄悄在入口处的草地上摘了一簇碎碎的小黄花,拈着它走向墓地。墓地太大了,它被划分了十几个区,白色的墓碑数不胜数,墓碑前几乎是没有鲜花的,不像我沿途经过的那些乡村小教堂旁的墓地,总有鲜花点缀着。我真不知该把花放在哪一座墓碑前。天气晴朗极了,阳光飞舞着,环绕着墓地的翠绿的松柏将它的影子投到草地上,就像为墓葬镶了一道花边。那里的游人零星可数,四周静悄悄的,只听得一片呢喃的乌语和草地下的大海的平静的呼吸声,我缓缓地独自穿行在墓地字架上的碑文,后来将那簇黄花献给了一个年龄只有十五岁的战士,十五岁--花季的年龄啊!
②有谁还会记忆着这些客死他乡的战士呢!他们无声无息地躺在这里,隔着苍茫的大海,诉说着他们永远的乡愁!他们的死亡,在历史教科书中,是伟大的辉煌的死亡。可是再崇高的定义,也不如生命本身的存在更富诗意,他们在最该对着青山碧海抒发豪情的年龄闭上了眼睛,在最该亲吻恋人的年龄闭上了嘴巴,所以我相信,他们年轻的心,一直没有死亡,大海上那些漂浮的云,可是他们流浪着的灵魂?他们该诅咒谁?诅咒制造了那场人间地狱的希特勒和墨索里尼?或者诅咒让他们成就英名的艾森豪威尔?
③在二战的将帅中,我最尊崇的人就是艾森豪威尔。凭着自己咄咄逼人的“战绩”,他成为一名五星上将,并且做了两届的美国总统。他的战绩之一,就是我面前的这片庞大的墓地,这样的战绩是多么的让人撕心裂肺啊!走在这样的墓地中,艾森豪威尔的光环在我心中黯淡了一圈,虽然我知道他仍然是一个伟大的 * * !。当我们折取橄榄枝的时候,其实对它已经构成了一种摧残。
④诺曼底登陆距今已有六十年了。为了纪念这个历史性的日子,在六月六日的一天,美国总统布什和英国首相布莱尔将莅,临诺曼底,祭奠他们长眠在这里的士兵。所以,诺曼底一带的公路正在为迎接这两国的领导人而加紧重修着。诺曼底一带旅馆的房价,也因此而提前几个月就开始了暴涨。当布什与布莱尔沿着平坦的道路畅通无阻地抵达这片墓地时,我相信这些越来越被世人所遗忘的战士的墓碑前会有鲜花覆盖着,庄严的祭奠的礼炮也会隆隆地响起。只是谁知他们带着怎样的情怀来到这里,但有一点可以肯定,他们的举动,将会使他们的政治天平中,又增加一个砝码!
⑤诺曼底的那片海域很美,可在我的眼里,它是我见过的世界上最苍凉的海岸!那飞起飞落的鸟,那飘来荡去的云,那在微风中摇曳着的松柏,那一望无际的墓碑,都在轻声诉说着一段已被我们逐渐遗忘看的历史,如果我们在阳光下看到了阴影,请不要惊诧,因为阴影从来就没有远离我们!
⑥我想起了艾森豪威尔在1953年就任美国第34任总统时发表的演说,他说:“在人类从黑暗走向光明的历程中,我们已经走了多远?我们是否正在接近光明,接近所有人类都应享有自由和平的一天?还是另一个黑暗的暗幕正在向我们逼近?”也许在他任职的四年中,他深深体会到了这样的黑暗仍然存在,所以他在1957年连任时又强调:“愿自由之光,普照一切黑暗的角落,燃起明亮的火焰,直到最终黑暗消失为止!”
⑦黑暗消失了吗?
⑧愿这样的墓葬能像火炬一样,照亮人间还残存的黑暗;让人类的光明,能像诺曼底的海水一样,汪洋澎湃,势不可挡! (有删改)
1.下列对文章的理解和分析,不正确的两项是[ ]
A.第②段结尾处一连串的问话,层层推进,增强语势,意在凸显作者对阵亡战士的深切怀念。
B.在作者看来布什、布莱尔祭奠长眠在这里的死者,给这里带来礼炮、鲜花的同时更给他们从政带来帮助。
C.本文以游踪为线,运用描写、议论、抒情的表达方式,融历史回顾与现实感怀于一体,引发读者思考。
D.第⑤段画线句子承上启下,引出艾森豪威尔相关的演说,其中“阴影”一词,既用本意,又用比喻义。
E.结尾段用“火炬”比喻墓葬,形象表达出作者对未来充满希望;用呼唤的口吻,有助于抒发强烈的情感。
2.简要分析第①段环境描写的作用。
_________________________________________________________________________________
3.联系全文,说说作者为什么以“最苍凉的海岸”为题?
_________________________________________________________________________________
4.“当我们折取橄榄枝的时候,其实对它已经构成了一种摧残”,联系实际,谈谈你对这句话的理解。(20字左右)
_________________________________________________________________________________
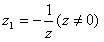 ,
,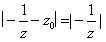 ,即
,即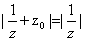 ,
,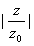 得
得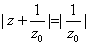 ,
,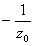 对应的点为圆心,
对应的点为圆心,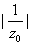 为半径的圆(除去原点)。
为半径的圆(除去原点)。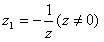 ,
,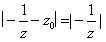 ,即
,即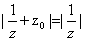 ,
,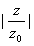 得
得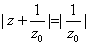 ,
,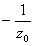 对应的点为圆心,
对应的点为圆心,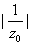 为半径的圆(除去原点)。
为半径的圆(除去原点)。