问题
计算题
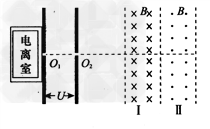
如图所示，电离室中存在大量密度相同、大小不同的球状纳米粒子，它们在电离室电离后均带正电，且所带电量与其表面积成正比。电离后的纳米粒子缓慢地通过小孔O1进入板间电压为U的电场加速后，又从小孔O2沿水平方向射入右方匀强磁场区域。已知匀强磁场区域I Ⅱ的水平宽度均为d，竖直方向足够长，磁感应强度大小均为B，方向分别垂直纸面向里和向外。设这些纳米粒子的最小半径为r0，其他粒子半径均为r0的整数倍，且半径最小的纳米粒子质量为m0、带电量为q0，不计纳米粒子的重力。已知球表面积公式S=4πr2，球体积公式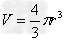
．求；
(1)半径为r0和2r0的纳米粒子经电场加速后速度之比；
(2)要使所有的纳米粒子均能穿过磁场区域，确定加速电压U应满足何条件；
(3)若加速电压取U0时，半径为r0的粒子恰好不能穿过磁场区域。求出这种情况下，半径为2r0的纳米粒子先后穿过磁场区域I和Ⅱ经历的总时间t。
答案
解：(1)根据动能定理
对半径为r0的粒子有
对半径为2r0的粒子有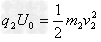
由题目条件知q2=4q0，m2=8m0
由以上三式得
(2)任意选取某质量为m、带电量为q的粒子来研究，设它在磁场中运动的半径为R
由
，
得
根据题目条件
，q=k·4πr2，故
正比于粒子半径r，由此知，半径为r0的粒子在磁场中做圆周运动的半径最小，只要它能穿过磁场，其他粒子均能穿过
即所有粒子均能穿过磁场的条件为
解得加速电压应满足的条件为
(3)半径为r0和半径为2r0的粒子轨迹分别如图中1、2所示
由上问可得两粒子在磁场中的半径分别为
，
根据题意R0=d，又q2=4q0，m2=8m0
得
设半径为2r0的粒子通过磁场区域I时，速度方向转过的角度为θ，则
得θ=45°
它穿过磁场区域I和Ⅱ经历的总时间