问题
解答题
选修42:矩阵与变换
已经矩阵M=.
(1)求直线4x-10y=1在M作用下的方程;
(2)求M的特征值与特征向量.
答案
(1) 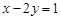 .
.
(2)当λ1=4时,由Mα1=λ1α1,得特征向量α1=;
当λ2=5时,由Mα2=λ2α2,得特征向量α2=.
本试题主要是考查了矩阵的运算,以及特征向量的求解和特征多项式的表示的综合运用。
(1)因为M=.设直线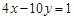 上任意一点
上任意一点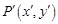 在作用下对应点
在作用下对应点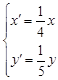 ,则 = ,
,则 = ,
(2)因为矩阵M的特征多项式f(λ)==(λ-4)(λ-5)=0,进而讨论得到特征向量。
(1)因为M=. 设直线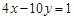 上任意一点
上任意一点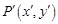 在作用下对应点
在作用下对应点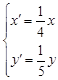 ,则 = ,………………………………………………………………2分
,则 = ,………………………………………………………………2分
即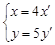 ,所以
,所以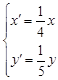 ,代入
,代入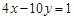 ,得
,得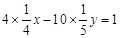 ,即
,即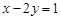 ,
,
所以所求曲线的方程为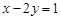 .……………………………………………………………4分
.……………………………………………………………4分
(2)矩阵M的特征多项式f(λ)==(λ-4)(λ-5)=0,
所以M的特征值为λ1=4,λ2=5. …………………………………………………………6分
当λ1=4时,由Mα1=λ1α1,得特征向量α1=;
当λ2=5时,由Mα2=λ2α2,得特征向量α2=.…………………………………………10分
