问题
填空题
设函数f(x)=(x+1)ln(x+1),若对所有的x≥0,都有f(x)≥a x成立,则实数a的取值范围为______.
答案
令g(x)=(x+1)ln(x+1)-ax,
对函数g(x)求导数:g′(x)=ln(x+1)+1-a
令g′(x)=0,解得x=ea-1-1,
(i)当a≤1时,对所有x>0,g′(x)>0,所以g(x)在[0,+∞)上是增函数,
又g(0)=0,所以对x≥0,都有g(x)≥g(0),
即当a≤1时,对于所有x≥0,都有f(x)≥ax.
(ii)当a>1时,对于0<x<ea-1-1,g′(x)<0,所以g(x)在(0,ea-1-1)是减函数,
又g(0)=0,所以对0<x<ea-1-1,都有g(x)<g(0),
即当a>1时,不是对所有的x≥0,都有f(x)≥ax成立.
综上,a的取值范围是(-∞,1].
故答案为(-∞,1].

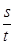 公式粗略地描述物体在一段时间内的运动情况,这个速度称为________________。
公式粗略地描述物体在一段时间内的运动情况,这个速度称为________________。