问题
问答题
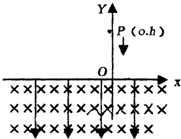
如图,在竖直平面内x轴下方有磁感强度为B,方向垂直纸面向里的匀强磁场和竖直向下的匀强电场,电场强度为E,一个带电小球从y轴上P(o.h)点以初速V0竖直向下抛出,小球穿过x轴后恰好作匀速圆周运动,重力加速度为g.求:(不知小球质量和电量)
(1)小球作圆周运动的半径.
(2)小球从P点出发开始计时,在什么时刻向下穿过x轴.
答案
(1)带电粒子由P到O,机械能守恒
即 mgh+
mV02=1 2
mV2①1 2
又∵mg=qE②
qVB=m
③V2 R
由①②③得:R=E Bg V02+2gh
(2)由P-O时间为t1
则有:t1=
④V-V0 g
粒子在电磁场中转半圆的时间为t2
则有:t2=1 2
=2πm qB
⑤πm qB
粒子向上离开电磁场到返回电磁时间为t3
则有:t3=
⑥2V g
那么粒子向下通过x轴的时间t
所以:t=t1+n(t2+t3)⑦
由①②③④⑤⑥⑦解得:t=
(1 g
-V0)+n(V02+2gh
+πE gB
)n=0、1、2、3…2 V02+2gh g
答:(1)小球作圆周运动的半径:R=E Bg
.V02+2gh
(2)小球从P点出发开始计时,在:t=
(1 g
-V0)+n(V02+2gh
+πE gB
)n=0、1、2、3…时刻向下穿过x轴.2 V02+2gh g
