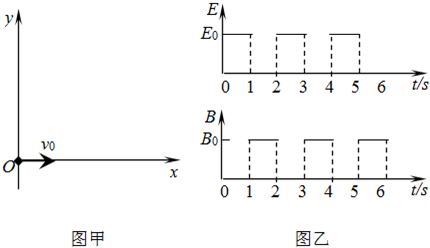
如图甲所示,在光滑绝缘的水平桌面上建立一xoy坐标系,平面处在周期性变化的电场和磁场中,电场和磁场的变化规律如图乙所示(规定沿+y方向为电场强度的正方向,竖直向下为磁感应强度的正方向).在t=0时刻,一质量为10g、电荷量为0.1C的带电金属小球自坐标原点O处,以v0=2m/s的速度沿x轴正方向射出.已知E0=0.2N/C、B0=0.2πT.求:
(1)t=1s末速度的大小和方向;
(2)1s~2s内,金属小球在磁场中做圆周运动的半径和周期;
(3)(2n-1)s~2ns(n=1,2,3,…)内金属小球运动至离x轴最远点的位置坐标.
(1)在0~1s内,金属小球在电场力作用下,在x轴方向上做匀速运动vx=v0,y方向做匀加速运动vy=t1
1s末粒子的速度v1==2m/s
设v1与x轴正方向的夹角为α,则tanα==1,故α=450
(2)在1s~2s内,粒子在磁场中做圆周运动,由牛顿第二定律,得qv1B0=,解得R1==m
粒子做圆周运动的周期T==1s
(3)粒子运动轨迹如图1所示
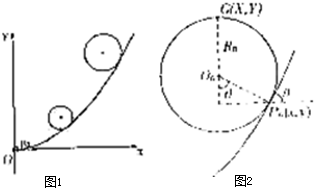
(2n-1)s末粒子的横坐标为x=v0t=2n(m)
纵坐标为:y=at2=××n2=n2(m)
此时粒子的速度为:vn==2 m/s
速度偏向角的正切值为:tanθ===n
带电粒子在(2n-1)s~2ns(n=1,2,3…)内做圆周运动的轨迹如图2所示,半径Rn==m
(2n-1)s~2ns(n=1,2,3,…)内粒子运动至离x轴最远点横坐标为:X=x-Rnsinθ=(2n-)m
纵坐标为:Y=y+Rn(1+cosθ)=(n2++)m
答:(1)t=1s末速度的大小为2m/s,方向与x轴成45°角;
(2)1s~2s内,金属小球在磁场中做圆周运动的半径为m,周期为1s;
(3)(2n-1)s~2ns(n=1,2,3,…)内金属小球运动至离x轴最远点的位置坐标为((2n-)m,(n2++)m).


