在竖直平面内放置一长为L、内壁光滑的薄壁玻璃管,在玻璃管的a端放置一个直径比玻璃管直径略小的小球,小球带电荷量为-q、质量为m.玻璃管右边的空间存在着匀强磁场与匀强电场.匀强磁场方向垂直于纸面向外,磁感应强度为B;匀强电场方向竖直向下,电场强度大小为
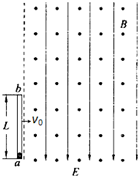
.如图所示,场的左边界与玻璃管平行,右边界足够远.玻璃管带着小球以水平速度v0垂直于左边界进入场中向右运动,由于水平外力F的作用,玻璃管进入场中速度保持不变,一段时间后小球从玻璃管b端滑出并能在竖直平面内运动,最后从左边界飞离电磁场.运动过程中小球的电荷量保持不变,不计空气阻力.mg q
(1)试分析小球在玻璃管中的运动情况;
(2)试求小球从玻璃管b端滑出时的速度大小;
(3)试求小球离开场时的运动方向与左边界的夹角.

(1)小球在玻璃管中沿水平方向做匀速直线运动
竖直方向做初速为零的匀加速直线运动 或小球做类平抛运动
(2)由E=
得,Eq=mg即重力与电场力平衡mg q
所以小球在管中运动的加速度为:a=
=Fy m Bv0q m
设小球运动至b端时的y方向速度分量为vy,则:
=2aLv 2y
所以小球运动至b端时速度大小为v=
L+2Bv0q m v 20
(3)设小球在管中运动的时间为t,小球在磁场中做圆周运动的半径为R,运动轨迹如图所示,
t时间内玻璃管的运动距离x=v0t
由牛顿第二定律得:qvB=mv2 R
由几何关系得:sinα=x-x1 R
因为,
=x1 R vy v
所以x1=
R=vy v
•qv0Bt mv
=v0t=xmv qB
可得sinα=0
故α=00,即小球飞离磁场时速度方向垂直于磁场边界向左
答:(1)小球做类平抛运动;
(2)则小球从玻璃管b端滑出时的速度大小为v=
;
L+2Bv0q m v 20
(3)则小球离开场时的运动方向与左边界的夹角为0.
