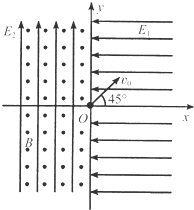
以竖直向上为y轴正方向的平面直角系xOy,如图所示.在第一、四象限内存在沿x轴负方向的匀强电场E1,在第二、三象限内存在着沿y轴正方向的匀强电场E2和垂直于xOy平面向外的匀强磁场.现有一质量为m、电荷量为q的带正电小球从坐标原点O以初速度v0沿与x轴正方向成45°角的方向射出.已知两电场的电场强度E1=E2=
,磁场的磁感应强度为B.mg q
(1)求小球离开O点后第一次经过y轴所用的时间;
(2)求小球离开O点后第三次经过y轴的坐标;
(3)若小球从O点以某一初速度沿与x轴正方向成135°角的方向射出且能再次回到O点,则该初速度的大小为多少?
(1)设小球在第一象限中的加速度为a,
由牛顿第二定律得
=ma(mg)2+(qE)2
得到a=
g,方向与v0的方向相反2
在第一象限中小球先匀减速运动再反向匀加速运动,所以
t1=
=2v0 a
v02 g
(2)小球第一次经过y轴后,在第二、三象限内由qE=mg,电场力与重力平衡,故做匀速圆周运动.设轨迹半径为R.有
qv0B=mv 20 R
得R=mv0 qB
小球第二次经过y轴的坐标
y1=
R=2
mv02 qB
t时间后第三次经过y轴,在第一、四象限内做类平抛运动,有
v0t′=1 2
gt22
得t′=
v02 g
小球第二次经过y轴与第三次经过y轴的距离为
△y=
v0t′=2 2v 20 g
小球第三次经过y轴的坐标y2=y1-△y=
-
mv02 qB 2v 20 g
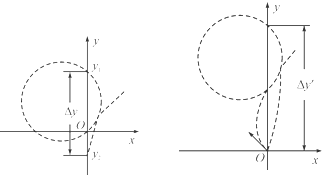
(3)若小球沿与x轴正方向成135°射出时小球的运动轨迹如图所示,有△y′=2
R′2
即
=22v2 g 2 mv qB
得v=
mg2 qB
答:(1)则小球离开O点后第一次经过y轴所用的时间
;
v02 g
(2)则小球离开O点后第三次经过y轴的坐标
-
mv02 qB
;2v 20 g
(3)若小球从O点以某一初速度沿与x轴正方向成135°角的方向射出且能再次回到O点,则该初速度的大小为
.
mg2 qB