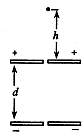
如图所示,中心带孔的平行板电容器水平放置,板长L=0.4m,板间距离为d=0.6m,两板间电压U=6V,使板间产生匀强电场(电场只存在于两板间).一带电微粒在正对小孔上方距小孔h=0.8m高处由静止释放,经t=0.55s从下极板小孔处穿出.(不计空气阻力,g=10m/s2)求:
(1)微粒进入上极板小孔时的速度及在两极板间运动的时间;
(2)若在两极板间再加一垂直纸面的匀强磁场,其他条件不变,微粒仍从原来位置由静止释放,为使微粒从两极板右侧偏出,求所加磁场的磁感应强度的方向及大小应满足的条件.
(1)微粒进入电场前做自由落体运动.设进入电场前速度为v,所用时间为t1,则h=
g1 2 t 21
v=gt1
设微粒在两极板间运动时间为△t,则△t=t-t1
代入数值后可得:
v=4m/s△t=0.15s
(2)未加磁场前,根据微粒在电场中运动时间,可判定在进入电场后做匀速运动.
Eq=mg
式中E=U d
加磁场B后,微粒做匀速圆周运动,若微粒恰好从上极板右边缘偏出,则微粒做圆周运动的半径为R1,则R1=L 4
若微粒恰好从下极板右边缘偏出,半径为R2,则利用几何关系得
=d2+(R2-R 22
)2L 2
利用qvB=mv2 R
代入数值后可解得:
4T≤B≤40T
根据未加磁场前微粒做匀速运动可判断微粒带负电,再利用左手定则可判断磁感应强度方向垂直纸面向外.
答:(1)微粒进入上极板小孔时的速度为4m/s,在两极板间运动的时间为0.15s.
(2)磁场的磁感应强度的方向垂直纸面向外,大小范围为4T≤B≤40T.
