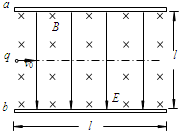
如图所示,水平放置的两块带电金属板a、b平行正对.极板长度为l,板间距也为l,板间存在着方向竖直向下的匀强电场和垂直于纸面向里磁感强度为B的匀强磁场.假设电场、磁场只存在于两板间的空间区域.一质量为m的带电荷量为q的粒子(不计重力及空气阻力),以水平速度v0从两极板的左端中间射入场区,恰好做匀速直线运动.求:
(1)金属板a、b间电压U的大小______
(2)若仅将匀强磁场的磁感应强度变为原来的2倍,粒子将击中上极板,求粒子运动到达上极板时的动能大小______
(3)若撤去电场,粒子能飞出场区,求v0满足的条件______
(4)若满足(3)中条件,粒子在场区运动的最长时间______.
(1)粒子匀速运动,受力平衡,根据受力平衡的条件可得:
q
=qv0B,U l
所以电压:
U=lv0B;
(2)仅将匀强磁场的磁感应强度变为原来的2倍,洛伦兹力变大,但是洛伦兹力与速度的方向垂直,洛伦兹力不做功,只有电场力对粒子做功,根据动能定理可得:
q•
U=1 2
mv2-1 2
mv021 2
又因为 U=lv0B
所以,粒子运动到达上极板时的动能大小为:
EK=
mv02+1 2
qBlv0;1 2
(3)当粒子恰好贴着右边界飞出时为速度的一个最值,
此时:圆心角为60度
则由几何关系可得r=
l3
由牛顿第二定律得:qv0B=mv 20 r
解得:v0=5qBl 4m
所以速度:
v0≥5qBl 4m
当粒子从左边界飞出时,粒子做的是半径r=
l的半圆,此时有:1 4
r=
l=1 4 mv0 qB
所以此时的速度v0≤
;qBl 4m
(4)由于T=
,与粒子的速度大小无关,所以圆心角为180度时运动时间最长,最长的时间为:2πm qB
t=
T=1 2 πm qB
故答案为:
(1)U=lv0B;
(2)EK=
mv02-1 2
qBlv0;1 2
(3)v0≤
或v0≥qBl 4m
;5qBl 4m
(4)
.πm qB
