问题
问答题
如图所示,质量为m,电量为q的带正电
的微粒以初速度v0垂直射入相互垂直的匀强电场和
匀强磁场中,刚好沿直线射出该场区,若同一微粒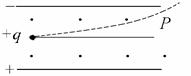
以初速度v0/2垂直射入该场区,则微粒沿图示的
曲线从P点以2v0速度离开场区,求微粒在场区中
的横向(垂直于v0方向)位移,(已知磁场的磁感应强度大小为B.)
答案
s=15mv0/(8qB).
速度为v0时粒子受重力、电场力和磁场力,三力在竖直方向平衡;速度为v0/2时,磁场力变小,三力不平衡,微粒应做变加速度的曲线运动.
当微粒的速度为v0时,做水平匀速直线运动,有: qE=mg+qv0B ①;
当微粒的速度为v0/2时,它做曲线运动,但洛伦兹力对运动的电荷不做功,只有重力和电场力做功,设微粒横向位移为s,由动能定理
(qE-mg)s=1/2m(2v0)2-1/2m(v0/2)2 ②.
将①式代入②式得qv0BS=15mv02/8,
所以s=15mv0/(8qB).
由于洛伦兹力的特点往往会使微粒的运动很复杂,但这类只涉及初、末状态参量而不涉及中间状态性质的问题常用动量、能量观点分析求解
