在相互垂直的匀强磁场和匀强电场中,有倾角为θ的足够光滑的绝缘斜面,磁感应强度为B,方向水平向外,电场强度E,方向竖直向上,有一质量为m、带电荷量为+q的小滑块,静止在斜面顶端时对斜面的正压力恰好为零,如图所示.
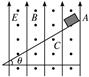
(1)如果迅速把电场方向转为竖直向下,求小滑块能在斜面上连续滑行的最远距离L和所用时间t.
(2)如果在距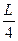 远处的C点放一个相同质量但不带电的小物体,当滑块从A点静止下滑到C点时,两物体相碰并黏合在一起,则此黏合体在斜面上还能再滑行多少时间和距离?
远处的C点放一个相同质量但不带电的小物体,当滑块从A点静止下滑到C点时,两物体相碰并黏合在一起,则此黏合体在斜面上还能再滑行多少时间和距离?
(1)L=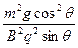 t=
t=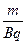 cotθ
cotθ
(2)s=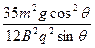 t′=
t′=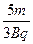 cotθ
cotθ
(1)只有一个滑块运动:由题意知电场方向竖直向上,Eq=mg,场强大小不变,转为竖直向下时,滑块沿斜面连续下滑的最大距离L可根据动能定理有:
(mg+Eq)Lsinθ=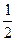 mv2
mv2
即2mgLsinθ=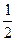 mv2 ①
mv2 ①
当滑块刚刚离开斜面时有
Bqv=(mg+Eq)cosθ
即v=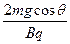 ②
②
①②式联立得:L=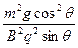
再根据动量定理可知t=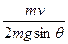 =
=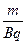 cotθ.
cotθ.
(2)两个物体先后运动,设在C点处碰撞前滑块的速度为v,则2mg× sinθ=
sinθ=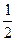 mv2 ③
mv2 ③
设碰撞后黏合体速度为u,由动量守恒有
mv="2mu " ④
当黏合体将要离开斜面时,有
Bv′q=(2mg+Eq)cosθ=3mgcosθ ⑤
据动能定理,碰后两物体共同下滑的过程
3mgssinθ=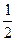 (2m)v′2-
(2m)v′2-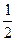 (2m)u2 ⑥
(2m)u2 ⑥
所以黏合体在斜面上还能滑行的距离由③④⑤⑥式联立得:s=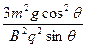 -
-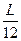
将L结果代入后整理有s=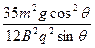
黏合体在斜面上还能滑行的时间可由动量定理求得:
t′=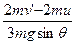 =
=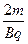 cotθ-
cotθ-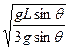
将L结果代入后整理有
t′=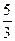 t=
t=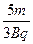 cotθ.
cotθ.
