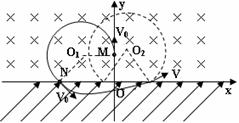
如图所示,在x轴上方整个区域有一磁感应强度B=0.5T,方向垂直纸面向里的匀强磁场,在x轴下方整个区域有一电场强度E= N/C,方向与y轴正方向成45°夹角的匀强电场,在t=0时刻有一比荷q/m="100" C/kg的带正电的粒子从y轴上的M点沿y轴正方向射入磁场,经磁场偏转后,从x轴上的N点(图中未标出)射入电场,已知M、N距原点O的距离分别为
N/C,方向与y轴正方向成45°夹角的匀强电场,在t=0时刻有一比荷q/m="100" C/kg的带正电的粒子从y轴上的M点沿y轴正方向射入磁场,经磁场偏转后,从x轴上的N点(图中未标出)射入电场,已知M、N距原点O的距离分别为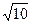 cm、(2
cm、(2 +
+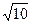 )cm,不计带电粒子在磁场和电场中的重力。求:
)cm,不计带电粒子在磁场和电场中的重力。求:
(1)带电粒子射入磁场的初速度V0;
(2)带电粒子第2次经过x轴的时刻及坐标;
(3)带电粒子第3次经过x轴的坐标;
(1)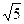 m/s(2)
m/s(2)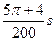 -(2
-(2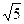 -
-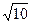 )cm(3)-(2
)cm(3)-(2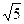 +
+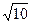 )cm
)cm
(1)设带电粒子第一次在磁场中做匀速圆周运动的半径为R1,圆心O1与N连线与x轴的夹角为α,
则有:R1+R1cosα =2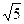 +
+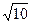
R1sinα =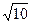
解得:R1 =2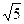 cm cosα =1/
cm cosα =1/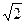 即α = 45°
即α = 45°
根据:qV0B=m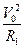 解得:V0=
解得:V0=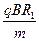 =100×0.5×2
=100×0.5×2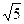 ×10-2=
×10-2=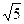 m/s
m/s
(2)因α = 45°,所以带电粒子进入匀强电场后将做类平抛运动,设带电粒子第2次经过x轴的位置P
则有:x′= V0t2
y′= 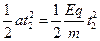
因α = 45°,所以有x′= y′
所以: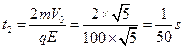
x′= V0t2=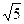 /50 m=2
/50 m=2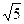 cm
cm
又因: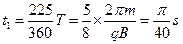
所以带电粒子第2次经过x轴的时刻为tP= t1+t2=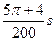
带电粒子第2次经过x轴的坐标为x P= xN+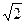 x′= -(2
x′= -(2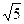 +
+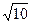 )+ 2
)+ 2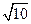 = -(2
= -(2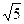 -
-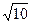 )cm
)cm
(3)带电粒子第2次经过x轴的速度分量分别为
Vx′=V0=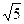 m/s
m/s
Vy′=at2=2V0=2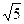 m/s
m/s
所以:V=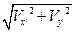 =
= 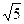 V0=5m/s
V0=5m/s
根据:qVB=m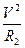 解得:R2=
解得:R2=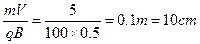
设V与E的夹角为β,则有tanβ=1/2
所以有带电粒子第3次经过x轴的坐标
x3="x" P-2R2sin(45°-β)=-(2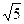 -
-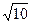 )-2×10×
)-2×10×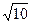 /10= -(2
/10= -(2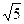 +
+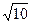 )cm
)cm
