问题
单项选择题
对于曲线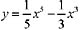
，下列各性态不正确的是：().
A．有3个极值点
B．有3个拐点
C．有2个极值点
D．对称原点
答案
参考答案：A
解析：
y'=x4-x2=x2(x2-1)=0，得x=-1，0，1。
验证这3个点是否都是极值点，
x=0_和x=0+时，y'均小于0，即符号相同，则点(0，0)不是极值点；
x=-1-和x=-1+时，y'符号不同，则点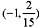
为极值点；
同理，点
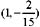为极值点
即有2个极值点，所以选项(A)错误。
画图如下，可看出有2个极佰点。
y"=(x4-x2)'=4x3-2x=2x(2x2-1)=0，得，和上面一样进行验证后知这三个均为拐点。
因为y是奇函数，所以对称原点。
[点评] 导数为0并不一定就是极值点，必须进行验证。