问题
解答题
二阶矩阵M对应的变换将点(1,-1)与(-2,1)分别变换成点(-1,-1)与(0,-2).设直线l在变换M作用下得到了直线m:2x-y=4,求l的方程.
答案
x+4=0
设M=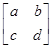 ,则有
,则有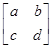
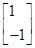 =
=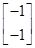 ,
,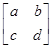
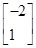 =
=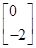 ,∴
,∴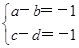 ,
,
且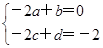 ,解得
,解得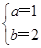 和
和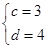 ,∴M=
,∴M=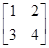 ,
,
∵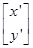 =
=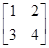
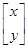 =
=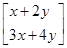 ,且m:2x′-y′=4,
,且m:2x′-y′=4,
∴2(x+2y)-(3x+4y)=4,即x+4=0,∴直线l的方程为x+4=0.
二阶矩阵M对应的变换将点(1,-1)与(-2,1)分别变换成点(-1,-1)与(0,-2).设直线l在变换M作用下得到了直线m:2x-y=4,求l的方程.
x+4=0
设M=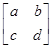 ,则有
,则有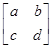
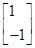 =
=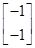 ,
,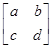
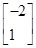 =
=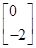 ,∴
,∴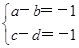 ,
,
且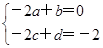 ,解得
,解得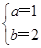 和
和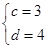 ,∴M=
,∴M=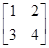 ,
,
∵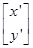 =
=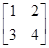
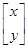 =
=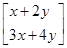 ,且m:2x′-y′=4,
,且m:2x′-y′=4,
∴2(x+2y)-(3x+4y)=4,即x+4=0,∴直线l的方程为x+4=0.