问题
解答题
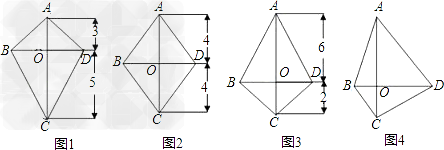
已知线段AC=8，BD=6．
（1）已知线段AC垂直于线段BD．设图1，图2和图3中的四边形ABCD的面积分别为S1、S2和S3，则S1=______，S2=______，S3=______；
（2）如图4，对于线段AC与线段BD垂直相交（垂足O不与点A，C，B，D重合）的任意情形，请你就四边形ABCD面积的大小提出猜想，并证明你的猜想；
（3）当线段BD与AC（或CA）的延长线垂直相交时，猜想顺次连接点A，B，C，D，A所围成的封闭图形的面积是多少？
答案
解：（1）S1=24，S2=24，S3=24；
（2）对于线段AC与线段BD垂直相交（垂足O不与点A，C，B，D重合）的任意情形，四边形ABCD的面积为定值24．
证明如下：∵AC⊥BD，
∴S△BAC=
AC·OB，S△DAC=
AC·OD，
∴S四边形ABCD=
AC·OB+
AC·OD=
AC·（OB+OD）=
AC·BD=24；
（3）顺次连接点A，B，C，D，A所围成的封闭图形的面积仍为24．
证明：∵AC⊥BD，
∴S△ABD=
AO·BD，S△BCD=
CO·BD，
∴S四边形ABCD=S△ABD+S△BCD=
AO·BD+
CO·BD=
BD（AO+CO）=
BD·AC=24．