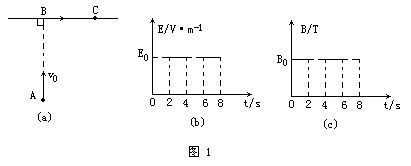
如图1(a)所示，在空间存在一个变化的电场和一个变化的磁场，电场的方向水平向右(图中由B到C)，场强的大小变化如图1(b)所示，磁感应强度变化如图1(c)所示，方向垂直于纸面，从t＝1s末开始，在A点每隔2s有一个相同的带电粒子(重力不计)沿AB方向(垂直于BC)的速度v0射出，恰好能击中C点，若AC＝2BC，且粒子在AC间的运动时间小于1s，求：
(1)图像中E0和B0的比值；
(2)磁场的方向；
(3)若第一个粒子击中C点的时刻已知为(1＋Δt)s，则第二个粒子击中C点的时刻是多少？
（1）
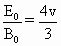（2）磁场方向垂直于纸面向外
(3)3＋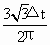
．
由题意可知，粒子在A与C之间运动的时间小于1s，也就是粒子在该区域运动时只有磁场或只有电场存在．当只有磁场存在时，粒子作匀速圆周运动，A，C两点的连线即为其轨迹所对应的弦，画出粒子运动的轨迹图．当只有电场时，粒子的运动可类似于平抛运动进行处理．
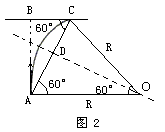
粒子在1s末进入该区域时，空间只有磁场，粒子运动的轨迹如图2所示．令BC＝L，由图可知
R＝AC＝2L．
粒子在磁场中运动时，洛伦兹力提供向心力．
qvB＝m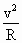
，
即 R＝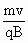
，则B0＝
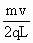，①
当粒子在电场中运动时，在AB方向上是匀速运动，在BC方向上是匀加速运动，则有
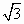L＝vt，L＝
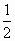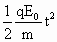at2＝
，②
由①②式得 E0＝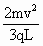
，③
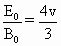由①③式得 ，④
由②④式得t＝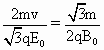
．⑤
(2)粒子带正电(它在电场中受到的电场力与电场方向相同)，由粒子在磁场中的偏转方向和左手定则可以判断磁场方向垂直于纸面向外．
(3)第一个粒子击中C点的时刻已知为(1＋Δt)s，该粒子是在磁场中运动，所需时间是由其轨迹对应的圆心角所确定的，由图可知粒子从A到C时，轨迹的圆心角为π/3，所以
Δt＝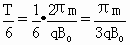
，⑥
由⑥式可得：
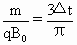
并将其代入⑤式，可得第二个粒子在电场中运动的时间为：
t＝，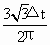
故第二个粒子击中C点的时刻为：
t2＝3＋t＝3＋．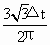
★ 试题错析： 思维诊断：此题的关键之处在于带电粒子在磁场或电场中运动时，由于它们的轨迹是经过相同的点，这点可以将场强和磁感应强度联系起来，这正是学生的思维障碍之处，所以要善于找到问题的联接处．
