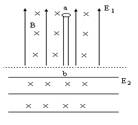
如图所示,虚线上方有场强为E1=6×104N/C的匀强电场,方向竖直向上,虚线下方有场强为E2的匀强电场,电场线用实线表示,另外,在虚线上、下方均有匀强磁场,磁感应强度相等,方向垂直纸面向里,ab是一长为L=0.3m的绝缘细杆,沿E1电场线方向放置在虚线上方的电、磁场中,b端在虚线上,将一套在ab杆上的带电量为q=-5×10-8C的带电小环从a端由静止释放后,小环先作加速运动而后作匀速运动到达b端,小环与杆间的动摩擦因数μ=0.25,不计小环的重力,小环脱离ab杆后在虚线下方仍沿原方向作匀速直线运动.
(1)请指明匀强电场E2的场强方向,说明理由,并计算出场强E2的大小;
(2)若撤去虚线下方电场E2,其他条件不变,小环进入虚线下方区域后运动轨迹是半径为L/3的半圆,小环从a到b的运动过程中克服摩擦力做的功为多少?
(1)电场方向向左,2.4×105N/C
(2)-3×10-4J
设匀强磁场的磁感应强度为B,带电粒子在虚线上方匀速运动速度为V,
(1)带电小环在虚线上方做匀速运动时,有
μBvq=qE1 (1)
带电小环在虚线下方做匀速运动,洛仑兹力的方向向左,由于小环做匀速运动,可知电场力方向应向右,电场方向向左
Bvq=qE2 (2)
解(1)、(2)得,E2=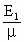 =
=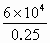 N/C=2.4×105N/C
N/C=2.4×105N/C
(2)若去掉虚线下方的电场后,带电小环做圆围运动,有
Bvq=m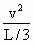 (3)
(3)
得 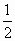 mV2=
mV2=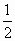 ×
×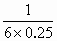 ×Bvq=
×Bvq=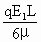
在虚线上方,电场力做功 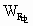 =qE1L
=qE1L
根据动能定理 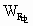 +Wf=
+Wf=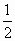 mV2-0
mV2-0
Wf=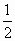 mV2-
mV2-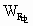 =
=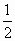 mV2-qE1L=
mV2-qE1L=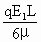 -qE1L
-qE1L
=(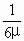 -1)qE1L=(
-1)qE1L=(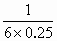 -1)×6×104×5×10-8×0.3J
-1)×6×104×5×10-8×0.3J
=-3×10-4J
