问题
计算题
在如图所示的直角坐标系中，一、四象限存在垂直于纸面向里的匀强磁场，磁感应强度为B，二、三象限存在沿y轴负方向的匀强电场。现有一质量为m、电量为q的带点粒子从x轴负半轴上坐标为(-x , 0 )的位置出发开始运动，速度大小为v0，方向沿x轴正方向，粒子只受电场和磁场力的作用。若要粒子能够回到出发点，电场强度应为多大？粒子需多长时间回到出发点？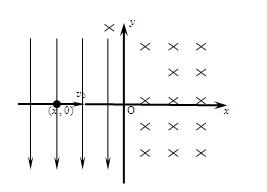
答案
粒子射入磁场之前，在x方向做匀速直线运动，在y方向做匀变速直线运动。设电场强度大小为E，则根据x方向的匀速运动可求出此段运动的时间
t1=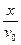
(2分)
根据y方向的匀变速直线运动规律，y方向的位移和末速度大小为
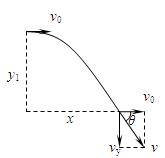
y1=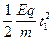
=
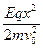(2分)
vy=
=
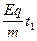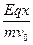(2分)
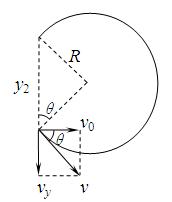
在磁场中粒子做匀速圆周运动，轨迹如图所示
由粒子在磁场中运动的规律，半径
R=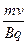
(2分)
粒子在y方向的位移大小
y2=2Rcosθ
=
=
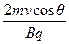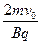(2分)
粒子离开磁场再次进入电场，在x方向做匀速直线运动，在y方向做匀变速直线运动。若能回到出发点，设此运动时间为t3。由x方向上做匀速直线运动
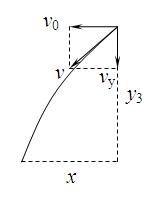
t3=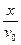
此阶段y方向做匀变速直线运动的位移
y3=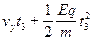
=
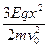(2分)
综合3段运动，粒子回到出发点，有
y1-y2+y3="0 " (2分)
代入以上结果可得
E=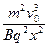
(1分)