(21分)
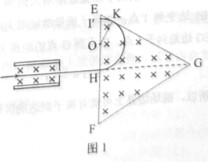
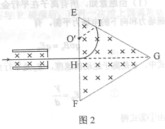
图中左边有一对平行金属板,两板相距为d,电压为V;两板之间有匀强磁场,磁感应强度大小为 ,方向平行于板面并垂直于纸面朝里。图中右边有一边长为a的正三角形区域EFG(EF边与金属板垂直),在此区域内及其边界上也有匀强磁场,磁感应强度大小为B,方向垂直于纸面朝里。假设一系列电荷量为q的正离子沿平行于金属板面、垂直于磁场的方向射入金属板之间,沿同一方向射出金属板之间的区域,并经EF边中点H射入磁场区域。不计重力。
,方向平行于板面并垂直于纸面朝里。图中右边有一边长为a的正三角形区域EFG(EF边与金属板垂直),在此区域内及其边界上也有匀强磁场,磁感应强度大小为B,方向垂直于纸面朝里。假设一系列电荷量为q的正离子沿平行于金属板面、垂直于磁场的方向射入金属板之间,沿同一方向射出金属板之间的区域,并经EF边中点H射入磁场区域。不计重力。

(1)已知这些离子中的离子甲到达磁场边界EG后,从边界EF穿出磁场,求离子甲的质量。
(2)已知这些离子中的离子乙从EG边上的I点(图中未画出)穿出磁场,且GI长为 。求离子乙的质量。
。求离子乙的质量。
(3)若这些离子中的最轻离子的质量等于离子甲质量的一半,而离子乙的质量是最大的,问磁场边界上什么区域内可能有离子到达。
(1)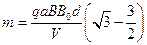
(2)
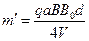
(3)所以,磁场边界上可能有离子到达的区域是: 边上从
边上从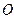 到
到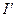 点。
点。 边上从
边上从 到
到 。
。
(21分)
(1)由题意知,所有离子在平行金属板之间做匀速直线运动,它所受到的向上的磁场力和向下的电场力平衡,有
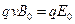 ①
①
式中,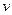 是离子运动的速度,
是离子运动的速度,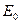 是平行金属板之间的匀强电场的强度,有
是平行金属板之间的匀强电场的强度,有
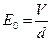 ②
②
由①②式得
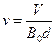 ③
③
在正三角形磁场区域,离子甲做匀速圆周运动。设离子甲质量为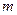 ,由洛仑兹力公式和牛顿第二定律有
,由洛仑兹力公式和牛顿第二定律有
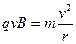 ④
④
式中,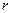 是离子甲做圆周运动的半径。离子甲在磁场中的运动轨迹为半圆,圆心为
是离子甲做圆周运动的半径。离子甲在磁场中的运动轨迹为半圆,圆心为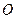 :这半圆刚好与
:这半圆刚好与 边相切于
边相切于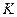 ,与
,与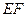 边交于
边交于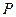 点。在
点。在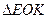 中,
中,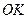 垂直于
垂直于 。由几何关系得
。由几何关系得

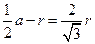 ⑤
⑤
由⑤式得

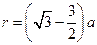 ⑥
⑥
联立③④⑥式得,离子甲的质量为
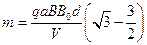 ⑦
⑦
(2)同理,由洛仑兹力公式和牛顿第二定律有
 ⑧
⑧
式中,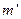 和
和 分别为离子乙的质量和做圆周运动的轨道半径。离子乙运动的圆周的圆心
分别为离子乙的质量和做圆周运动的轨道半径。离子乙运动的圆周的圆心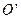 必在
必在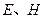 两点之间,又几何关系有
两点之间,又几何关系有
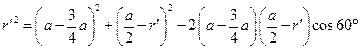 ⑨
⑨
由⑨式得
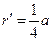 ⑩
⑩
联立③⑧⑩式得,离子乙的质量为
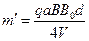 (11)
(11)
(1) 对于最轻的离子,其质量为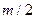 ,由④式知,它在磁场中做半径为
,由④式知,它在磁场中做半径为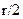 的匀速圆周运动。因而与
的匀速圆周运动。因而与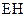 的交点为
的交点为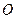 ,有
,有
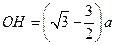 (12)
(12)
(2)当这些离子中的离子质量逐渐增大到m时,离子到达磁场边界上的点的位置从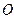 点沿
点沿 边变到
边变到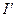 点;当离子质量继续增大时,离子到达磁场边界上的点的位置从
点;当离子质量继续增大时,离子到达磁场边界上的点的位置从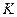 点沿
点沿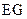 边趋向于
边趋向于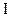 点。
点。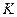 点到
点到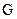 点的距离为
点的距离为
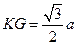 (13)
(13)
(3)所以,磁场边界上可能有离子到达的区域是: 边上从
边上从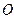 到
到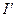 点。
点。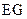 边上从
边上从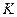 到
到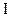 。
。
