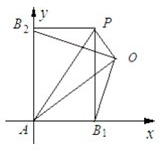
根据条件知A，B₁，P，B₂构成一个矩形A，B₁PB₂，以AB₁，AB₂所在直线为坐标轴建立直角坐标系，设|AB₁|=a，|AB₂|=b，点O的坐标为（x，y），则点P的坐标为（a，b），

由

OB1

=

OB2

=1，得

(x-a)2+y2=1 x2+(y-b)2=1

，则

(x-a)2=1-y2 (y-b)2=1-x2

∵|

OP

|＜

1

2

，∴(x-a)2+(y-b)2＜

1

4

∴1-x2+1-y2＜

1

4

∴x2+y2＞

7

4

①

∵（x-a）²+y²=1，∴y²=1-（x-a）²≤1，

∴y²≤1

同理x²≤1

∴x²+y²≤2②

由①②知

7

4

＜x2+y2≤2，

∵|

OA

|=

x2+y2

，∴

7

2

＜|

OA

|≤

2

故选D．