问题
计算题
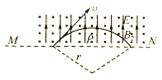
如图所示,水平地面上有一辆小车,车上固定一个竖直光滑绝缘管,管的底部有一质量 、电荷量
、电荷量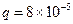 C的
C的 带正电小球,小球的直径比管的内径略小。
带正电小球,小球的直径比管的内径略小。
在管口所在水平面 的下方存在着垂直纸面向里、磁感应强度
的下方存在着垂直纸面向里、磁感应强度 的匀强磁场,
的匀强磁场, 面的上方还存在着竖直向上、场强
面的上方还存在着竖直向上、场强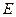 =25V/m的匀强电场和垂直纸面向外、磁感应强度
=25V/m的匀强电场和垂直纸面向外、磁感应强度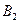 =5T的匀强磁场,现让小车始终保持
=5T的匀强磁场,现让小车始终保持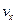 =2m/s的速度匀速向右运动,以带电小球刚经过磁场的边界
=2m/s的速度匀速向右运动,以带电小球刚经过磁场的边界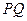 为计时的起点,测得小球在管内运动的这段时间为
为计时的起点,测得小球在管内运动的这段时间为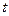 =
=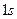 ,
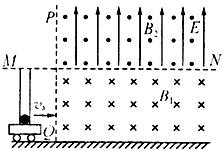
,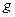 取10/
取10/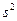 ,不计空气阻力。
,不计空气阻力。
(1)求小球进入磁场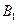 时的加速度
时的加速度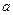 的大小。
的大小。
(2)求小球离开管口时的速度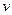 的大小。
的大小。
(3)若小球离开管口后,求该小球离开MN平面的最大距离是多少?
答案
(1)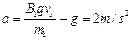
(2)
(3)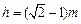
(1)小球在管中参与两个方向的运动,
即:水平方向,以 向右匀速运动;
向右匀速运动;
竖直方向,因水平速度而受到竖直向上的洛伦兹力,向上匀加速运动。
所以小球进入磁场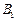 时的加速度
时的加速度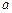 由牛顿第二定律有
由牛顿第二定律有
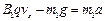 ,代入数据得
,代入数据得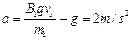
(2)小球在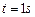 时,竖直分速度
时,竖直分速度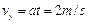 ,而水平分速度
,而水平分速度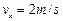
则小球离开管口的速度
(3)小球离开管子后,进入MN上方的复合场中,因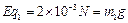
所以小球在洛伦兹力的作用下做匀速圆周运动,设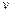 与MN成
与MN成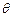 角
角
则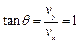 ,所以
,所以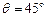
其运动的轨迹如右图所示
由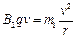 ,得
,得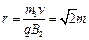
当小球运动到最高点时,速度水平。
设最高点距MN的距离为 ,则
,则