问题
单项选择题
已知
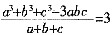，则(a-b)2+(b-c)2+(a-b)(b-c)的值为( )
答案
参考答案：C
解析： a3+b3+c3-3abc=[(a+b)3-3a2b-3ab2]+c3-3abc
=(a+b)3+c3-(3a2b+3ab2+3abc)
=(a+b+c)[(a+b)2-(a+b)c+c2]-3ab(a+b+c)
=(a+b+c)(a2+b2+c2-ab-ac-bc)
=3(a+b+c)
所以a2+b2+c2-ab-ac-bc=3，(a-b)2+(b-c)2+(a-b)(b-c)=a2+b2+c2-ab-ac-bc=3。