问题
计算题
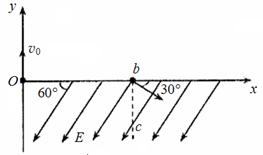
（21分）如图所示，x轴上方存在磁感应强度为B的圆形匀强磁场区域，磁场方向垂直纸面向外（图中未画出）。x轴下方存在匀强电场，场强大小为E，方向沿与x轴负方向成60°角斜向下。一个质量为
m，带电量为＋e的质子以速度v0从O点沿y轴正方向射入匀强磁场区域。质子飞出磁场区域后，从b点处穿过x轴进入匀强电场中，速度方向与x轴正方向成30°，之后通过了b点正下方的c点。不计质子的重力。
（1）画出质子运动的轨迹，并求出圆形匀强磁场区域的最小半径和最小面积；
（2）求出O点到c点的距离。
答案
（1）
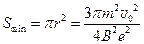
（2）
（1）质子先在匀强磁场中做匀速圆周运动， 射出磁场后做匀速直线运动，最后进入匀强电场做类平抛运动，轨迹如图所示.根据牛顿第二定律，有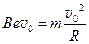
。。。。（2分）
要使磁场的区域面积最小，则Oa为磁场区域的直径，由几何关系可知：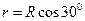
。。。。。。。。。。。。（2分）
求出圆形匀强磁场区域的最小半径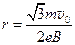
。。。。。。。。（2分）
圆形匀强磁场区域的最小面积为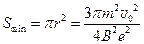。。。。。。。。。（3分）
（2）质子进入电场后，做类平抛运动，垂直电场方向：
。。。。。（2分）
平行电场方向：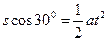
。。。。。。。。。。。。。。。。。。（2分）
由牛顿第二定律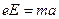
。。。。。。。。。。。。。。。。。。。 （2分）
解得：
。。。。。。。。。。。。。。。。。（2分）
O点到c点的距离：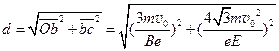
。。。。。。。 （4分）