问题
计算题
如图16所示，x轴正方向水平向右，y轴正方向
竖直向上．在xOy平面内有与y轴平行的匀强电场，在半径为R的圆内还有与xOy平面垂直的匀强磁场．在圆的左边放置一带电微粒发射装置，它沿x轴正方向发射出一束具有相同质量m、电荷量为q(
q>0)和初速度为v的带电微粒．发射时，这束带电微粒分布在0<y<2R的区间内。已知重力加速度大小为g，若从A点射出的带电微粒平行于x轴从C点进入磁场区域，并从坐标原点O沿y轴负方向离开。
（1）求电场强度和磁感应强度
的大小；
（2）请指出这束带电微粒与x轴相交的区域，并指出这束带电微粒中哪些粒子在磁场中运动的时间最长；最长时间为多少？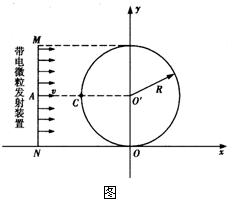
答案
（1）带电粒子
平行于x轴从C点进入磁场，说明带电微粒所受重力和电场力平衡．设电场强度大小为E，由mg=qE可得E=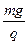
，方向沿y轴正方向． (2分)
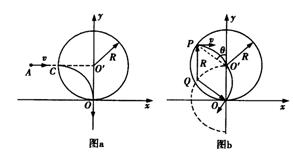
带电微粒进入磁场后，将做圆周运动，且r=R．如图a所示．设磁感应强度大小为B
由牛顿第二定律得: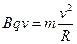
(2分)
解得：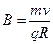
(2分)
（2）这束带电微粒都通过坐标原点 (1分)
从任一点P水平进入磁场的带电微粒在磁场中做半径为R的匀速圆周运动．如图b所示，P点与O/点的连线与y轴的夹角为θ，则圆心Q的坐标为(－Rsinθ，Rcosθ)，
又数学知识得：粒子圆周运动的轨迹方程为：(x+Rsinθ)
2+(y—Rcosθ)2="R2 "
令y=0， 解得x="0 " (2分)
因所有的粒子最后从原点离开，且半径均为R，所以从M点进入的粒子在磁场中偏转的角度为180°最大，因而运动的时间最长。(2分)
又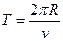
则时间tm=
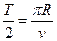(1分)