问题
解答题
某儿童服装店欲购进A、B两种型号的儿童服装。经调查：B型号童装的进货单价是A型号童装的进货单价的两倍，购进A型号童装60件和B型号童装40件共用去2100元。
（1）求A、B两种型号童装的进货单价各是多少元？
（2）若该店每销售1件A型号童装可获利4元，每销售1件B型号童装可获利9元，该店准备用不超过6300元购进A、B两种型号童装共300件，且这两种型号童装全部售出后总获利不低于1795元。问该店应该怎样安排进货，才能使总获利最大？最大总获利为多少元？
答案
解：（1）设A型号童装的进货单价为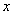
元，则B型号童装的进货单价为
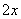元，
根据题意，得 60x+40×2x=2100，
解方程，得x=15，则2x=30，
答：A、B两种型号童装的进货单价分别是15元、30元。
（2）设该店购进A型号童装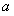
件，则购进B型号童装（300-
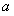）件，
由题意，得
，
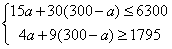解得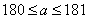
，
∵总获利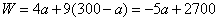
，
∴W是关于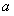
的一次函数，并且W随
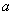的增大而减小，
故当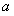
=180时，W最大，此时W=-5×180+2700=1800，
此时，30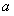0-
=120。
答：该店应购进A型号童装180件，B型号童装120件，才能使总获利最大，最大总获利为1800元。