问题
选择题
物体在万有引力场中具有的势能叫做引力势能。若取两物体相距无穷远时的引力势能为零，一个质量为m0的质点到质量为M0的引力源中心的距离为r0时，其万有引力势能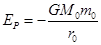
（式中G为引力常数）。一颗质量为m的人造地球卫星以半径为r1的圆形轨道环绕地球匀速飞行，已知地球的质量为M，要使此卫星绕地球做匀速圆周运动的轨道半径增大为r2，则卫星上的发动机所消耗的最小能量为：（假设卫星的质量始终不变，不计空气阻力及其它星体的影响）：
A．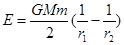
B．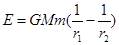
C．
D．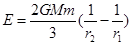
答案
答案：A
题目分析：设卫星轨道半径为r时，
由：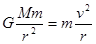
（M为地球的质量）
由题目条件 其引力势能为：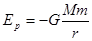 
卫星在在r处时的总能量（动能与引力势能之和）为：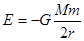
故半径为r1时，卫星总能量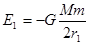
故半径为r2时，其总能量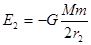
由功能关系关系得：卫星轨道变化过程中克服阻力的功
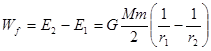，选项A正确；故选A
点评：本题中等难度。引力势能实际是重力势能的另一种表现形式，克服阻力做的功等于卫星损失的机械能（动能与引力势能之和），千万注意不要丢了动能