(供选学物理3-1的考生做)(8分)
如图所示,M、N为正对着竖直放置的金属板,其中N板的正中央有一个小孔,M、N板间的电压U1 = 1.0×103 V.P、Q为正对着水平放置的金属板,板长L =" 10" cm,两板间的距离d =" 12" cm,两板间的电压U2 =" 2.4" × 103 V.P、Q板的右侧存在方向垂直纸面向里的匀强磁场区域,其中虚线为磁场的左右边界,边界之间的距离l =" 60" cm,竖直方向磁场足够宽.一个比荷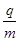 = 5.0×104 C/kg的带正电粒子,从静止开始经M、N板间的电压U1加速后,沿P、Q板间的中心线进入P、Q间,并最终进入磁场区域.整个装置处于真空中,不计重力影响.
= 5.0×104 C/kg的带正电粒子,从静止开始经M、N板间的电压U1加速后,沿P、Q板间的中心线进入P、Q间,并最终进入磁场区域.整个装置处于真空中,不计重力影响.
(1)求粒子进入P、Q板间时速度υ 的大小;
(2)若粒子进入磁场后,恰好没有从磁场的右边界射出,求匀强磁场的磁感应强度B的大小.
(1)粒子在M、N间运动时,根据动能定理得
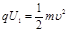
粒子进入P、Q板间时速度υ=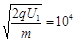 m/s
m/s
 (2)设粒子在P、Q板间运动的时间为t.
(2)设粒子在P、Q板间运动的时间为t.
粒子的加速度 
粒子在竖直方向的速度υy = a t
粒子的水平位移 L= υ t
若粒子穿出P、Q板间时速度偏向角为θ,则
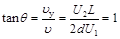
所以θ = 45°.
粒子穿出P、Q板间时的速度υ1=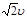
粒子在匀强磁场中做匀速圆周运动时,轨迹如图所示,
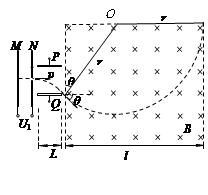
粒子进入磁场时速度的大小为υ1,速度的方向与水平方向的夹角也为θ,所以
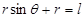
因为洛伦兹力提供向心力,则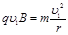
解得 B = 0.8 T
按其它方法正确解答的,同样得分。可参照本评分标准分步给分。最后结果有单位的,必须写明单位,单位写错、缺单位的扣1分。
