问题
解答题
已知函数f(x)=x3+ax2+bx+c,曲线y=f(x)在x=1处的切线为l:3x-y+1=0,当x=
(1)求a、b、c的值; (2)求y=f(x)在[-3,1]上的最大值和最小值. |
答案
(1)由f(x)=x3+ax2+bx+c,得
f′(x)=3x2+2ax+b
当x=1时,切线l的斜率为3,可得2a+b=0.①
当x=
时,y=f(x)有极值,则f′(2 3
)=0,2 3
可得4a+3b+4=0.②
由①、②解得a=2,b=-4.
由于l上的切点的横坐标为x=1,
∴f(1)=4.∴1+a+b+c=4.
∴c=5.
(2)由(1)可得f(x)=x3+2x2-4x+5,
∴f′(x)=3x2+4x-4.
令f′(x)=0,得x=-2,或x=
.2 3
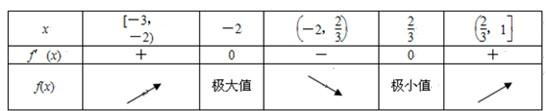
∴f(x)在x=-2处取得极大值f(-2)=13.
在x=
处取得极小值f(2 3
)=2 3
.95 27
又f(-3)=8,f(1)=4.
∴f(x)在[-3,1]上的最大值为13,最小值为
.95 27
