如图甲所示,水平放置足够长的平行金属导轨,左右两端分别接有一个阻值为R的电阻,匀强磁场与导轨平面垂直,质量m =" 0.1" kg、电阻r =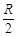 的金属棒置于导轨上,与导轨垂直且接触良好。现用一拉力F =(0.3+0.2t)N作用在金属棒上,经过2s后撤去F,再经过0.55s金属棒停止运动。图乙所示为金属棒的v–t图象,g = 10m/s2。求:
的金属棒置于导轨上,与导轨垂直且接触良好。现用一拉力F =(0.3+0.2t)N作用在金属棒上,经过2s后撤去F,再经过0.55s金属棒停止运动。图乙所示为金属棒的v–t图象,g = 10m/s2。求:
小题1:金属棒与导轨之间的动摩擦因数;
小题2:整个过程中金属棒运动的距离;
小题3:从 撤去F到金属棒停止的过程中,每个电阻R上产生的焦耳热。
撤去F到金属棒停止的过程中,每个电阻R上产生的焦耳热。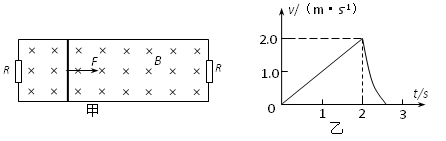
小题1: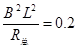
小题2: m
m
小题3: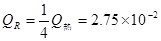 J
J
(1)在0-2s这段时间内,根据牛顿第二定律 有
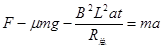 (2分)
(2分)
由图可知  (1分)
(1分)
又因 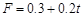
联立解得 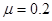 ,
, (1分)
(1分)
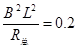
 (1分)
(1分)
(2) 在0--2s这段时间内的位移为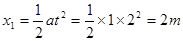 (1分)
(1分)
设棒在2---2.55s时间内的位移为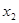 ,
,
棒在 t时刻,根据牛顿第二定律 有
 (1分)
(1分)
在t到t+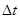 (
(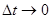 )时间内
)时间内
 (1分)
(1分)
 (1分)
(1分)
 (1分)
(1分)
代入数据得 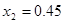 m
m
整个过程中金属棒运动的距离 m (1分)
m (1分)
(3)从撤去拉力到棒停止的过程中,根据能量守恒定律 有
 (2分)
(2分)
 J (1分)
J (1分)
每个电阻R上产生的焦耳热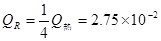 J (2分)
J (2分)
