(15分)如图甲所示,两平行金属板间接有如图乙所示的随时间t变化的交流电压u,金属板间电场可看做均匀、且两板外无电场,板长L=0.2m,板间距离d=0.1m,在金属板右侧有一边界为MN的匀强磁场,MN与两板中线OO′ 垂直,磁感应强度 B=5×10-3T,方向垂直纸面向里。现有带正电的粒子流沿两板中线OO′连续射入电场中,已知每个粒子的比荷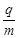 =108C/kg,重力忽略不计,在0-0.8×10-5s时间内两板间加上如图乙所示的电压(不考虑极板边缘的影响)。已知t = 0时刻进入两板间的带电粒子恰好在0.2×10-5s时刻经极板边缘射入磁场。(不考虑粒子间相互影响及返回板间的情况)。
=108C/kg,重力忽略不计,在0-0.8×10-5s时间内两板间加上如图乙所示的电压(不考虑极板边缘的影响)。已知t = 0时刻进入两板间的带电粒子恰好在0.2×10-5s时刻经极板边缘射入磁场。(不考虑粒子间相互影响及返回板间的情况)。
求:
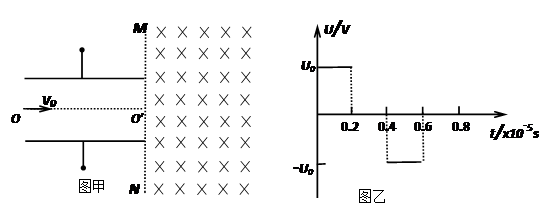
(1)求两板间的电压U0
(2)0-0.2×10-5s时间内射入两板间的带电粒子都能够从磁场右边界射出,求磁场的最大宽度
(3)若以MN与两板中线OO′ 垂直的交点为坐标原点,水平向右为x轴,竖直向上为y轴建立二维坐标系,请写出在0.3×10-5s时刻射入两板间的带电粒子进入磁场和离开磁场(此时,磁场只有左边界,没有右边界)时的位置坐标。
(4)两板间电压为0,请设计一种方案:让向右连续发射的粒子流沿两板中线OO′射入,经过右边的待设计的磁场区域后,带电粒子又返回粒子源。
(1)250 V/m(2)0.2 m(3)若向上偏转:进入坐标为 ( 0 ; 0.0125 ) (m)
离开磁场左边界坐标为 ( 0 ; 0.4125 ) (m) 若向下偏转:进入坐标为 ( 0 ; - 0.0125 ) (m) 离开磁场左边界坐标为 ( 0 ; 0.3875) (m) (4)见解析
(1) (3分)电荷在电场中作类平抛运动
d/2=at2/2 (1分) a="d/" t2=2.5×1010 (m/s2)
Eq="ma " (1分) E=ma/q=2.5×1010/108 ="250" (V/m)
U0="Ed=250×0.1=25" (V) (1分)
(2) (3分) 在0---0.2×10-5S时间内, 0.2×10-5S时刻射入两板间的带电粒子进入磁场并能够从磁场右边界射出,则其他粒子也都能从磁场的右边界射出。粒子进入磁场作匀速圆周运动,则:
Bqv=mv2/R1 R1=mv0/Bq (1分)
由第一问可知:v0=L/t=0.2/0.2×10-5 =105 (m/s) (1分)
R1=105/5×10-3×108="0.2" (m)
磁场的最大宽度为 D=R1=0.2 (m) (1分)
(3) (7分) 0.3×10-5S时刻进入的粒子先做匀速直线运动,再做类平抛运动. 类平抛运动时间应为t=0.1×10-5S .
若向上偏转,根据平抛运动公式得: y1=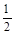 at2=2.5×1010×(0.1×10-5)2/2="0.0125" (m) (1分)
at2=2.5×1010×(0.1×10-5)2/2="0.0125" (m) (1分)
进入坐标为 ( 0 ; 0.0125 ) (m) (1分)
进入磁场作匀速圆周运动, R2="mv/Bq"
离开磁场时的坐标 y2=y1+2R2cosθ=y1+2 mv0/Bq
y2=0.0125+2×105/5×10-3×108="0.4125" (m)(1分)
离开磁场左边界坐标为 ( 0 ; 0.4125 ) (m) (1分)
若向下偏转,根据平抛运动公式得: y1=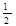 at2=2.5×1010×(0.1×10-5)2/2="0.0125" (m)
at2=2.5×1010×(0.1×10-5)2/2="0.0125" (m)
进入坐标为 ( 0 ; - 0.0125 ) (m) (1分)
进入磁场作匀速圆周运动, R2="mv/Bq"
离开磁场时的坐标 y2= 2R2cosθ- y1=" 2" mv0/Bq- y1
y2=2×105/5×10-3×108-0.0125="0.3875(m)" (1分)
离开磁场左边界坐标为 ( 0 ; 0.3875) (m) (1分)
(4) (2分)(只要合理均给分)

