如图所示，在垂直于光滑水平地面的竖直线A1A2的右侧的广阔区域，分布着竖直向上的匀强电场和平行于地面指向读者的匀强磁场。在地面上停放着一辆质量为M的绝缘小车，车的左、右两端竖直固定着一对等大的平行带电极板（构成电容为C的平行板电容器，板距为L），分别带电荷量为+Q和—Q，其中右极板紧靠A1A2线，下端开有一小孔。现有一带正电的小物块（电荷量为q、质量为m），从A1A2线上距右板下端小孔高为H处，以速度 v0水平向右射入电、磁场区域，恰在竖直平面内做圆周运动，且正好从右板下端的小孔切入小车底板的上表面，并立即贴着上表面滑行，但不会与左板相碰。已知小物块与车板面间的动摩擦因数为μ，两极板和小物块的电荷量始终保持不变，当地重力加速度为g。求：
小题1:A1A2线右侧电场的场强E和磁场的磁感应强度B的大小；
小题2:小物块在小车内运动离小车右板的最大距离。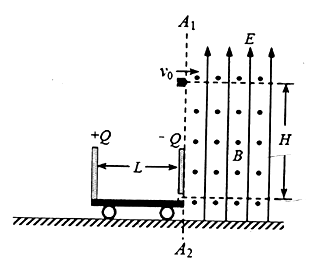
小题1: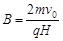
小题2: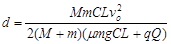
（1）由小物块在竖直平面内做圆周运动可知：
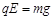①（1分）
解得：
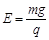（1分）
物块在竖直平面内做圆周运动的半径：
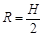②（1分）
根据牛顿第二定律及洛伦兹力公式：
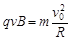③（1分）
由以上两式解得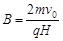： （1分）
（2）设两极板间匀强电场的场强为E0，两板间电压为U，则：
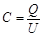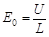④（1分）
⑤（1分）
设物块进入小车的加速度大小为a1，方向向右，根据牛顿第二定律：
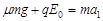⑥（1分）
设小车的加速度大小为a2，方向向左，根据牛顿第二定律：
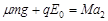⑦（1分）
设物块和小车达共同速度所需时间为t，根据运动学公式：
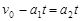⑧（1分）
设物块滑至距右板的最大距离为d，则：
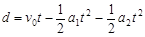⑨（1分）
联立以上各式解得：
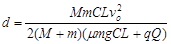⑩（1分）