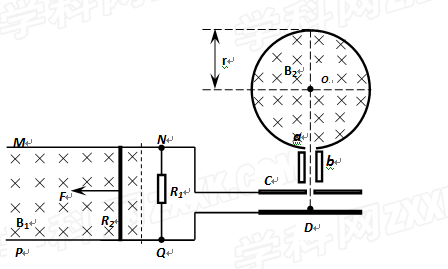
如图所示(俯视),MN和PQ是两根固定在同一水平面上的足够长且电阻不计的平行金属导轨.两导轨间距为L=0.2m,其间有一个方向垂直水平面竖直向下的匀强磁场B1=5.0T.导轨上NQ之间接一电阻R1=0.40Ω,阻值为R2=0.10Ω的金属杆垂直导轨放置并与导轨始终保持良好接触.两导轨右端通过金属导线分别与电容器C的两极相连.电容器C紧靠准直装置b,b紧挨着带小孔a(只能容一个粒子通过)的固定绝缘弹性圆筒.圆筒壁光滑,筒内有垂直水平面竖直向下的匀强磁场B2,O是圆筒的圆心,圆筒的内半径r=0.40m.
(1)用一个方向平行于MN水平向左且功率恒定为P=80W的外力F拉金属杆,使杆从静止开始向左运动.已知杆受到的摩擦阻力大小恒为Ff=6N,求:当金属杆最终匀速运动时杆的速度大小及电阻R1消耗的电功率?
(2)当金属杆处于(1)问中的匀速运动状态时,电容器C内紧靠极板的D处的一个带正电的粒子经C加速、b准直后从a孔垂直磁场B2并正对着圆心O进入筒中,该带电粒子与圆筒壁碰撞四次后恰好又从小孔a射出圆筒.已知该带电粒子每次与筒壁发生碰撞时电量和能量都不损失,不计粒子的初速度、重力和空气阻力,粒子的荷质比q/m=5×107(C/kg),则磁感应强度B2多大(结果允许含有三角函数式)?
(1) (2)见解析
(2)见解析
(1)金属杆先做加速度变小的加速运动,最终以最大速度匀速运动.设杆匀速运动时速度为v,回路中的感应电流为I,杆受到的安培力大小为FA,电阻R1消耗的电功率为P1,则
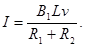 (1)
(1) 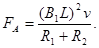 (2)
(2)  (3)
(3)
联立(2)(3)得: 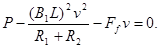 (4)
(4)
将已知数据代入(4)式解得:  ……(4分)
……(4分)
以及:  ……(1分)
……(1分)
(2)设杆匀速运动时C两极板间的电压为U,带电粒子进入圆筒的速率为V、在磁场中作匀速圆周运动的半径为R,由于C与电阻R1并联,
据欧姆定律得, 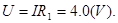
据动能定理有, 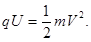 (5)
(5)
带电粒子在磁场中作匀速圆周运动,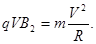 (6)
(6)
联立(5)(6)得: 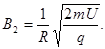 (7)……(4分)
(7)……(4分)
由于带电粒子与圆筒壁碰撞时无电量和能量损失,那么每次碰撞前后粒子速度大小不变、速度方向总是沿着圆筒半径方向,4个碰撞点与小孔a恰好将圆筒壁五等分,粒子在圆筒内的轨迹具有对称性,由5段相同的圆弧组成,设每段轨迹圆弧对应的圆心角为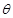 ,则由几何关系可得:
,则由几何关系可得:
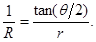 (8)……(1分)
(8)……(1分)
有两种情形符合题意(如图所示):
(ⅰ)情形1:每段轨迹圆弧对应的圆心角为 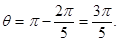
联立(7)(8)并代入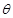 值得:
值得: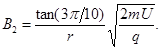 (9)
(9)
将数据代入(9)式得: 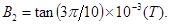 (10)……(4分)
(10)……(4分)
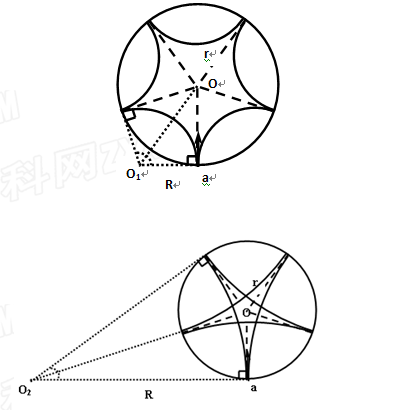
(ⅱ)情形2:每段轨迹圆弧对应的圆心角为 
联立(7)(8)并代入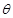 值得:
值得: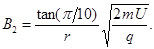 (11)
(11)
将数据代入(11)式得: 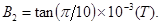 (12)……(4分)
(12)……(4分)
