如图所示，两平行的、间距为d的光滑金属导轨b1b2b3b4、c1c2c3c4分别固定在竖直平面内，整个导轨平滑连接，b2b3、c2c3位于同一水平面(规定该水平面的重力势能为零)，其间有一边界为b2b3c3c2、方向竖直向上的匀强磁场，磁感应强度大小为B，导轨两端均连有电阻为R的白炽灯泡。一长为d的金属杆PN与两导轨接触良好，其质量为m、电阻为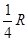
。若金属杆从导轨左侧某一位置开始以初速度v0滑下，通过磁场区域后，再沿导轨右侧上滑至其初始位置高度一半时速度恰为零，此后金属杆做往复运动。金属杆第一次通过磁场区域的过程中，每个灯泡产生的热量为Q，重力加速度为g，除金属杆和灯泡外其余部分的电阻不计。求：
(1)金属杆第一次通过磁场区域的过程中损失的机械能；
(2)金属杆初始位置的高度；
(3)金属杆第一次刚进入磁场区域时加速度的大小。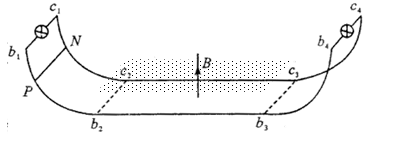
（1）
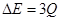（2）
（3）
（1）设金属杆第一次通过磁场区域的过程损失的机械能为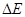
灯泡的并联电阻为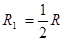
①
回路的总电阻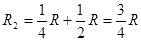
②
由焦耳定律得：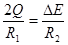
③
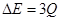由①②③得 ④
（2）设金属杆开始下滑时的高度为h
全程由能量转化和守恒定律有：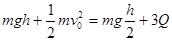
⑤
得： ⑥
（3）设金属杆第一次刚进入磁场区域时速度是v1 ，加速度为a，
金属杆刚进入磁场区域时产生的电动势为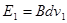
⑦
回路电流
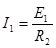⑧
金属杆受到的安培力为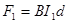
⑨
由牛顿第二定律有：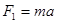
⑩
由机械能守恒定律有：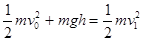
⑾
联立②⑥⑦⑧⑨⑩⑾得 ⑿