问题
计算题
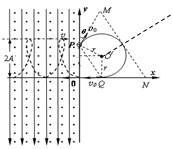
如图所示，质量为m，带电量为q（q>0）的粒子（重力不计），从离坐标原点为1.5a的 y轴上的P点，以速度大小为v0，方向与y轴正方向成θ=30°射入xoy坐标的第一象限，经过一个在第一象限内，边界形状为等腰梯形方向与xoy坐标面垂直匀强磁场区域，然后沿-x方向经过坐标原点0，进入相互垂直的匀强电场和匀强磁场中，其运动轨迹为虚线所示，该电场强度为E，方向沿-y轴方向，磁感应强度为B，方向垂直坐标面向外。
（1）画出最小的等腰梯形所处的位置和粒子运动轨迹，并求出此时的磁感应强度；
（2）粒子过坐标原点0后的运动可分解为x方向和y方向两分运动组成，已知y方向分运动为简谐运动；求粒子离x轴最远距离。
答案
（1）见解析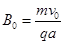 
（2）
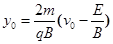
（1）设带电粒子垂直进入磁感应强度为B的匀强磁场中，轨迹半径为r，则有
① （2分）
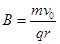② （1分）
最小的当等腰梯形边界如图PMNQ所示， ③（2分）
设：此时半径为r0 ，最大磁感应强度为B0
从图中可得 r0+r0sinθ=1.5a ④ （2分）
∴ r0=a ⑤（1分）
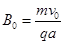⑥ （2分）
（2）设粒子运动到最高点速度为v，离x轴的距离为y0
根据动能定理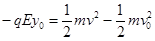 
⑦ （2分）
根据简谐运动的对称性，粒子在最低点和最高点加速度大小相同，方向相反，设最大加速度为a0，
根据牛顿第二定律： 在0点：qv0B-qE = ma ⑧（2分）
在最高点：qvB+qE=ma ⑨（2分）
由⑧⑨式解得：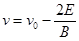
⑩（2分）
由⑦⑩解得 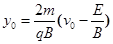（2分）