问题
计算题
如图所示，电阻可忽略导线框abcd固定在竖直平面内，导线框ab和dc的宽度为l，在bc段接入阻值为R的电阻，ef是一电阻可忽略的水平放置的导电杆，杆的质量为m，杆的两端分别与ab和cd保持良好接触，且能沿导线框ab和dc无摩擦地滑动，磁感应强度为B的匀强磁场方向与框面垂直. 现用一恒力F竖直向上拉导体杆ef，当导体杆ef上升高度为h时，导体杆ef恰好匀速上升，求：
（1）此时导体杆ef匀速上升的速度v的大小；
（2）导体杆ef上升h的整个过程中产生的焦耳热Q的大小.
答案
（1）
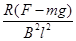（2）(F-mg)h –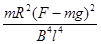
根据平衡及法拉第电磁感应定律求出速度；再根据能量守恒求出焦耳热。
（1）导电杆匀速上升时，受到竖直向上的恒力F，竖直向下的安培力F安和重力mg，
根据平衡条件有 F-mg- F安=0 (2分)
F安=BIl (1分)
根据法拉第电磁感应定律有 E="Blv" (2分)
根据闭合电路欧姆定律有 I=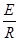 
(2分)
由以上各式联立解得 v= 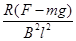(2分)
（2）导体杆上升h的整个过程中，根据能量守恒定律有
Q="(F-mg)h" -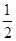 
mv2 (2分)
代入v= 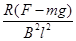得：
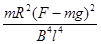Q ="(F-mg)h" – (2分)