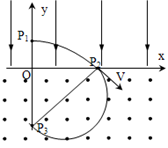
(18分)如图所示,在y>0的空间中存在匀强电场,场强沿y轴负方向;在y<0的空间中,存在匀强磁场,磁场方向垂直xy平面(纸面)向里.一电量为q、质量为m的带正电的运动粒子,经过y轴上y=h处的点P1时速率为V0,方向沿x轴正方向;然后,经过x轴上x=2h处的P2点进入磁场,并经过y轴上y=-2h处的P3点.不计重力.求:
(1)电场强度的大小.
(2)粒子到达P2时速度的大小和方向.
(3)磁感应强度的大小.
(1)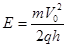 (2)
(2) ,θ=450(3)
,θ=450(3)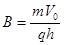
(1)粒子在电场、磁场中运动的轨迹如图所示.设粒子从P1到P2的时间为t,电场强度的大小为E,粒子在电场中的加速度为a,
由牛顿第二定律及运动学公式有:qE=ma, V0t=2h, h=at2/2 (3分)
由以上三式求得: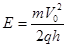 (2分)
(2分)
(2)粒子到达P2时速度沿x方向的分量仍为V0,,以V1表示速度沿y方向分量的大小,V表示速度的大小,θ表示速度和x轴的夹角,
则有:V12=2ah, V=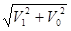 , tanθ=V1/V0 (3分)
, tanθ=V1/V0 (3分)
由以上三式可求得: ,θ=450 (2分)
,θ=450 (2分)
(2)设磁场的磁感应强度为B,在洛仑兹力作用下做匀速圆周运动,
设r是圆周的半径,由牛顿第二定律可得:BqV=mV2/r (2分)
此圆周与x轴和y轴的交点分别为P2、P3.因为OP2=OP3,θ=450,由几何关系可知,连线P2P3为圆轨道的直径,由此可求得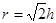 (3分)
(3分)
由以上各式可求得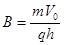 (3分)
(3分)
