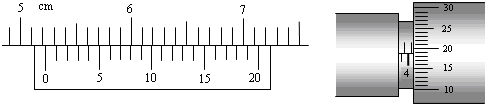
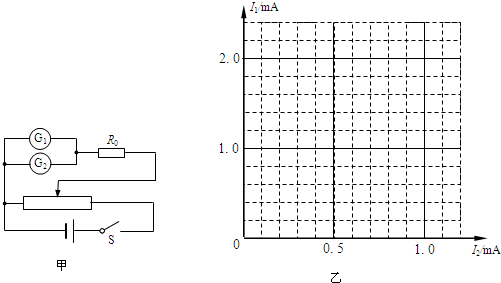
(16分)如图所示为某一仪器的部分原理示意图,虚线OA、OB关于y轴对称,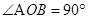 , OA、OB将xOy平面分为Ⅰ、Ⅱ、Ⅲ三个区域,区域Ⅰ、Ⅲ内存在水平方向的匀强电场,电场强度大小相等、方向相反。带电粒子自x轴上的粒子源P处以速度v0沿y轴正方向射出,经时间t到达OA上的M点,且此时速度与OA垂直。已知M到原点O的距离OM = a,不计粒子的重力。求:
, OA、OB将xOy平面分为Ⅰ、Ⅱ、Ⅲ三个区域,区域Ⅰ、Ⅲ内存在水平方向的匀强电场,电场强度大小相等、方向相反。带电粒子自x轴上的粒子源P处以速度v0沿y轴正方向射出,经时间t到达OA上的M点,且此时速度与OA垂直。已知M到原点O的距离OM = a,不计粒子的重力。求:

(1)匀强电场的电场强度E的大小;
(2)为使粒子能从M点经Ⅱ区域通过OB上的N点,M、N点关于y轴对称,可在区域Ⅱ内加一垂直xOy平面的匀强磁场,求该磁场的磁感应强度的最小值和粒子经过区域Ⅲ到达x轴上Q点的横坐标;
(3)当匀强磁场的磁感应强度取(2)问中的最小值时,且该磁场仅分布在一个圆形区域内。由于某种原因的影响,粒子经过M点时的速度并不严格与OA垂直,成散射状,散射角为 ,但速度大小均相同,如图所示,求所有粒子经过OB时的区域长度。
,但速度大小均相同,如图所示,求所有粒子经过OB时的区域长度。
(1)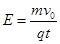 (2)(
(2)(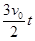 ,0)(3)2
,0)(3)2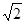 v0tsinθ
v0tsinθ
(1)粒子在Ⅰ区域内做类平抛运动,
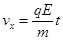 (1分)
(1分)
vx= v0 (1分)
解得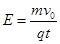 (1分)
(1分)
(2) 粒子在Ⅰ区域内在y方向上的位移y1= v0t (1分)
OM=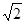 y1=
y1=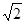 v0t (1分)
v0t (1分)
粒子在Ⅱ区域内做匀速圆周运动,其轨道半径R≤OM1=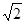 v0t (1分)
v0t (1分)
又因为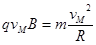 (1分)
(1分)
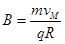 ≥
≥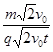 =
=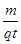 ,即Bmin=
,即Bmin=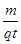 (1分)
(1分)
粒子进入Ⅲ区域后,其运动轨迹NQ与PQ对称,则OQ=OP=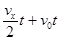 =
=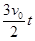
所以Q点的坐标为(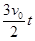 ,0) (1分)
,0) (1分)
速度方向沿负y方向 (1分)
(3)该圆形磁场区域的半径r等于其轨迹圆半径R,即r=R=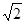 v0t (2分)
v0t (2分)
所有粒子出磁场时速度方向平行,其落点在直线OB上的GH两点之间,如图(2分)
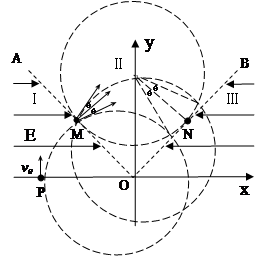
GH=2rsinθ=2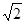 v0tsinθ (2分)
v0tsinθ (2分)