问题
计算题
（22分）如图所示的平行板器件中，存在相互垂直的匀强磁场和匀强电场，磁场的磁感应强度B1 =" 0.40" T，方向垂直纸面向里，电场强度E = 2.0×105 V/m，PQ为板间中线．紧靠平行板右侧边缘xOy坐标系的第一象限内，有垂直纸面的矩形匀强磁场区域，磁感应强度B2 =" 0.25" T。一束带电量q = 8.0×10-19 C，质量m = 8.0×10-26 kg的正离子从P点射入平行板间，不计重力，沿中线PQ做直线运动，穿出平行板后从y轴上坐标为（0，0.2m）的Q点垂直y轴射向矩形磁场区，离子通过x轴时的速度方向与x轴正方向夹角为60°。则：
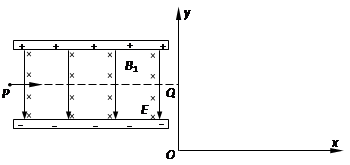
（1）离子运动的速度为多大？
（2）试讨论矩形区域内的匀强磁场方向垂直纸面向里和垂直纸面向外两种情况下，矩形磁场区域的最面积分别为多少？并求出其在磁场中运动的时间。
答案
（1）5×105 m/s（2）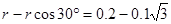
（1）由于离子直线穿过平行板器件， B1qv=Eq ---------（3分）
可得 v="E/" B1=5×105 m/s------------(3分)
（2）根据 B2 qv=mv2/r---------（1分）可知
离子在磁场B2中圆周运动的半径r=mv/qB2=0.2m-------（2分）
若磁感应强度B2的方向垂直纸面向外，
根据几何关系（如图），
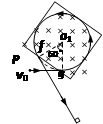
矩形的区域的最小长a=r=0.2m-----(1分)
矩形的区域的最小宽b=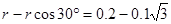 m-----(1分)
矩形的区域的最小面积为：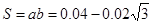
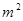-----(2分)
此时离子在磁场中运动的时间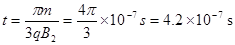
-------（3分）
若磁感应强度B2的方向垂直纸面向里，
由数学知识可知，矩形最小长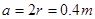
--(1分)
矩形最小宽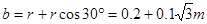
--(1分)
矩形的区域的最小面积为：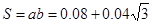
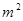-----(2分)
此时离子在磁场中运动的时间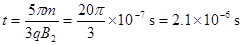
-------（3分）