问题
选择题
如图所示,质量相同的三颗卫星a、b、c绕地球做匀速圆周运动,其中b、c在地球的同步轨道上,a距离地球表面的高度为R,此时a、b恰好相距最近,已知地球质量为M、半径为R、地球自转的角速度为ω。引力常量为G,则

A.发射卫星b的速度要大于11.2km/s
B.卫星a的机械能小于卫星b的机械能
C.卫星a和卫星b下一次相距最近还需经过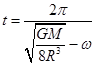
D.若要卫星c与卫星b实现对接,可让卫星c加速
答案
BC
题目分析:11.2km/s是第二宇宙速度,也就是使物体挣脱地球引力的最小的发射速度,发射同步卫星,发射速度应大于第一宇宙速度,小于第二宇宙速度(环绕速度),故A错误;卫星从较低圆轨道进入较高圆轨道要给卫星增加能量,此过程中卫星的动能减小,引力势能增大,故可知,较高轨道上的卫星其机械能大于较低轨道卫星的机械能,所以B正确;根据万有引力定律、牛顿第二定律有: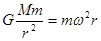 ,代入数据解得卫星a的角速度
,代入数据解得卫星a的角速度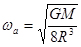 ,卫星a卫星b下一次相距最近时,a比b多转一圈,需用时,
,卫星a卫星b下一次相距最近时,a比b多转一圈,需用时,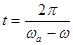 ,所以C正确;若要实现对接,两者一定要在不同轨道上,在低轨道上的卫星加速离心运动,向高轨道靠拢对接,或在高轨道卫星减速近心运动,向低轨道靠拢对接,在一轨道上的卫星不可能实现对接,因为一旦c加速,将做离心运动,故D错误。
,所以C正确;若要实现对接,两者一定要在不同轨道上,在低轨道上的卫星加速离心运动,向高轨道靠拢对接,或在高轨道卫星减速近心运动,向低轨道靠拢对接,在一轨道上的卫星不可能实现对接,因为一旦c加速,将做离心运动,故D错误。
